itgle.com

设随机变量X1，X2，…，Xn相互独立，Sn=X1+X2+…+Xn，则根据列维一林德伯格中心极限定理，当n充分大时，Sn近似服从正态分布，只要X1，X2，…，Xn( )。A．有相同的数学期望B．有相同的方差C．服从同一指数分布D．服从同一离散型分布

题目

设随机变量X1，X2，…，Xn相互独立，Sn=X1+X2+…+Xn，则根据列维一林德伯格中心极限定理，当n充分大时，Sn近似服从正态分布，只要X1，X2，…，Xn( )。

A．有相同的数学期望

B．有相同的方差

C．服从同一指数分布

D．服从同一离散型分布

相似考题

1.设X1，X2，…，Xn是简单随机样本，则有( )。A．X1，X2，…，Xn相互独立B．X1，X2，…，Xn有相同分布C．X1，X2，…，Xn彼此相等D．X1与(X1+X2)/2同分布E．X1与X2的均值相等

2.设总体X～N(2，42)，(x1，x2，…，Xn)是来自X的简单随机样本，则下面结果正确的是( )。A．B．C．D．

3.设X1，X2，…，Xn是来自正态总体N(μ，σ2)的一个样本，则有( )。

4.数列X1，X2，…，XP存在极限可以表述为：对任何ε＞0，有N＞0，使任何n，m＞N，有│Xn-Xm＜ε。数列X1，X2，…，XP不存在极限可以表述为(57)。A．对任何ε＞0，有N＞0，使任何n，m＞N，有│Xn-Xm≥εB．对任何ε＞0，任何N＞0，有n，m＞N，使│Xn-Xm≥εC．有ε＞0，对任何N＞0，有n，m＞N，使│Xn-Xm≥εD．有ε＞0，N＞0，对任何n，m＞N，有│Xn-Xm≥ε

更多“设随机变量X1,X2,…,Xn相互独立,Sn=X1＋X2＋…＋Xn,则根据列维一林德伯格中心极限定理,当n充分大时,Sn ”相关问题

  • 第1题：

    设X1，X2，…，Xn是一个样本，样本的观测值分别为x1，x2，…，xn，则样本方差s2的计算公式正确的有( )。


    正确答案：ACD
    解析：

  • 第2题：

    对于随机变量X1,X2,…,Xn,下列说法不正确的是().


    答案：D
    解析：
    若X1，X2，…，Xn相互独立，则(B)，(C)是正确的，若X1，X2，…，Xn两两不相关，则(A)是正确的，选(D).

  • 第3题：

    设(X1,X2,…,Xn)是抽自正态总体N(u,σ2)的一个容量为10的样本，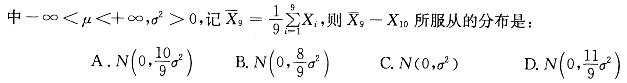


    答案：A
    解析：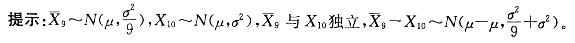

  • 第4题：

    设X1,X2,…Xn是简单随机样本，则有（ ）。
    A. X1,X2,…Xn相互独立 B. X1,X2,…Xn有相同分布
    C. X1,X2,…Xn彼此相等 D.X1与(X1,+X2)/2同分布
    E.X1与Xn的均值相等


    答案：A,B,E
    解析：
    简单随机样本满足随机性和独立性，且每一个样本都与总体同分布，样本均值相等。

  • 第5题：

    设总体X服从参数为2的指数分布，X1，X2，…，Xn为来自总体X的简单随机样本，则当n→∞时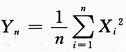，依概率收敛于_______.


    答案：
    解析：
    本题是数三的考题，根据切比雪夫大数定律或者辛钦大数定律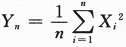，依概率收敛于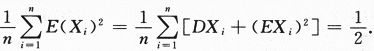答案应填

  • 第6题：

    若随机变量x1,x2,…,xn相互独立同分布于N{μ,2^2},则根据切比雪夫不等式得P{｜x－μ｜≥2）≤_______.


    答案：
    解析：
    因为X1，X2…，Xn相互独立同分布于N（μ，2^2），所以，从而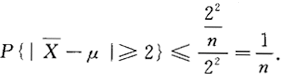

  • 第7题：

    设总体X~N(0,σ2)，X1，X2，...Xn是自总体的样本，则σ2的矩估计是:


    答案：D
    解析：
    提示 注意 E(x)=0，σ2=D(x)=E(x2) - [E(x)]2=E(x2)，σ2也是x的二阶原点矩，σ2的矩估计量是样本的二阶原点矩。

  • 第8题：

    设样本x1，x2，…，xn来自正态总体N（0，9），其样本方差为s2，则E（s2）=（）


    正确答案:9

  • 第9题：

    设X1，X2，…，Xn是从总体X中抽取的容量为n的一个样本，如果由此样本构造一个函数T（X1，X2，…，Xn），不依赖于任何未知参数，则函数T（X1，X2，…，Xn）是一个（）


    正确答案:统计量

  • 第10题：

    问答题
    设总体X～N(μ,σ2)，x1,x2,…xn为其样本，为样本均值,则____．

    正确答案：
    解析：

  • 第11题：

    问答题
    设A为n阶方阵，若对任意n维向量x(→)＝（x1，x2，…，xn）T都有Ax(→)＝0。证明：A＝0。

    正确答案：
    由对任意n维向量x(→)都有Ax(→)=0,知对基本单位向量组ε(→)1,ε(→)2,…,ε(→)n,Aε(→)i=0(i=1,2,…,n)成立。
    所以有A(ε(→)1,ε(→)2,…,ε(→)n)=0,即AE=0,故A=0。
    解析： 暂无解析

  • 第12题：

    问答题
    设X1，X2，…，Xn相互独立且同服从分布B（1，p），Z＝X1＋X2＋…＋Xn，证明Z～B（n，p）。

    正确答案：
    利用数学归纳法。
    当k=2时,X1+X2=Z~B(2,p)。
    假设当k=n-1时,X1+X2+…+Xn-1=Z1~B(n-1,p)。
    则当k=n时,Z=(X1+X2+…+Xn-1)+Xn=Z1+Xn,Z~B(n-1+1,p),即Z~B(n,p)。
    解析： 暂无解析

  • 第13题：

    设X1,X2,…,Xn,…相互独立,则X1,X2,…,Xn,…满足辛钦大数定律的条件是( )




    A.X1,X2,…,Xn,…同分布且有相同的数学期望与方差
    B.X1,X2,…,Xn,…同分布且有相同的数学期望
    C.X1,X2,…,Xn,…为同分布的离散型随机变量
    D.X1,X2,…,Xn,…为同分布的连续型随机变量

    答案：B
    解析：
    根据辛钦大数定律的条件，应选(B).

  • 第14题：

    设随机变量X1，X2，…，Xn相互独立，Sn=X1，X2，…，Xn则根据列维林德伯格(Levy-Lindberg)中心极限定理，当n充分大时，Sn近似服从正态分布，只要1，X2，…，Xn

    A.有相同的数学期望.
    B.有相同的方差.
    C.服从同一指数分布.
    D.服从同一离散分布.

    答案：C
    解析：
    【简解】本题是数四的考题，答案应选(C).

  • 第15题：

    设X1，X2，…，Xn，…为独立同分布的随机变量列，且均服从参数为λ(λ>1)的指数分布，记φ(x)为标准正态分布函数，则



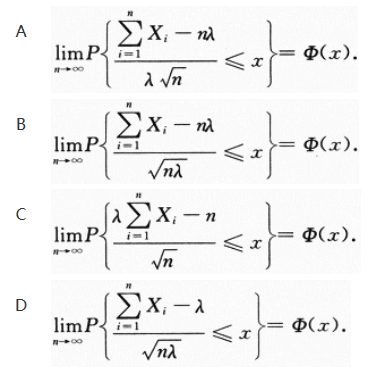    答案：C
    解析：
    【简解】本题是数四的考题.X1，X2，…，Xn，…独立同分布、方差存在.根据中心极限定理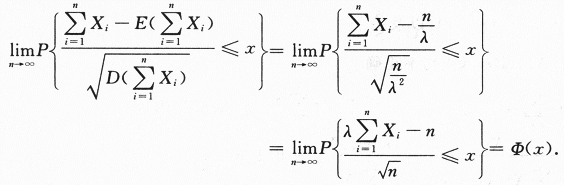　　

  • 第16题：

    设随机变量X1,X2,…,Xn相互独立且在［0,na］上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.


    答案：
    解析：

  • 第17题：

    设X1,X2,…,Xn是来自总体X的简单随机样本,已知E(X^k)=ak(k=1,2,3,4).
    　　证明：当n充分大时,随机变量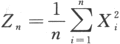近似服从正态分布,并指出其分布参数.


    答案：
    解析：

  • 第18题：

    设总体X～N（μ,σ^2）,X1,X2,…,xn为总体的简单样本,S^2为样本方差,则D(S^2)=_______.


    答案：
    解析：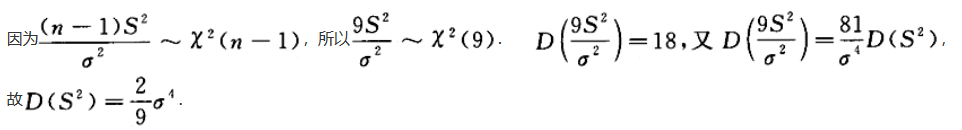

  • 第19题：

    设X1，X2...，Xn是来自总体的简单随机样本，则X1，X2，...，Xn必然满足（）

    • A、独立但分布不同
    • B、分布相同但不相互独立
    • C、独立同分布
    • D、不能确定

    正确答案:C

  • 第20题：

    关于中心极限定理的描述正确的是：（）。

    • A、对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布
    • B、正态样本均值服从分布N（μ，σ2/n）
    • C、设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布
    • D、无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布

    正确答案:A,B,C,D

  • 第21题：

    多选题
    关于中心极限定理的描述正确的是：（）。
    A

    对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布

    B

    正态样本均值服从分布N（μ，σ2/n）

    C

    设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布

    D

    无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布


    正确答案： C,D
    解析： 暂无解析

  • 第22题：

    多选题
    设X1，X2，…，Xn是简单随机样本，则有(　　)。
    A

    X1，X2，…，Xn相互独立        

    B

    X1，X2，…，Xn有相同分布

    C

    X1，X2，…，Xn彼此相等，      

    D

    X1与（X1+X2）/2同分布

    E

    X1与Xn的均值相等


    正确答案： C,A
    解析： 暂无解析

  • 第23题：

    问答题
    设函数f（x）在（a，b）内连续，a＜x1＜x2＜…＜xn＜b，证明：必∃ξ∈（a，b），使f（ξ）＝[f（x1）＋f（x2）＋…＋f（xn）]/n。

    正确答案：
    设f(x)在[x1,xn]上的最大值为M,最小值为m。
    则由题设可知,f(x)在[x1,xn]上连续,则它在[x1,xn]上必有最大值和最小值,则m≤[f(x1)+f(x2)+…+f(xn)]/n≤M。
    由最值介值定理可知,必∃ξ∈[x1,xn]⊂(a,b),使得f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。
    解析： 暂无解析

相关内容