itgle.com

设y=cos4x，则dy=（　　）

题目
设y=cos4x，则dy=（　　）


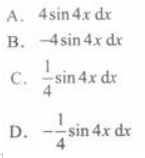
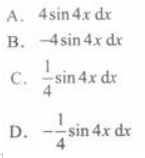
相似考题

1.设X~N(3,42),且Y=3X＋4,则DY等于()。A、27B、25C、144D、43

2.设(X,Y)相互独立,EX=EY=0,DX=DY=1,则E(X＋Y＋1)^2=5。()此题为判断题(对，错)。

3.设y=ln（cosx），则微分dy等于：

4.设函数y=y(x)由方程y+arcsinx=ex+y确定。求dy.

更多“设y=cos4x，则dy=（　　） ”相关问题

  • 第1题：

    设y=f(t)，t=φ(x)都可微，则dy=( )。

    A.f′(t)dt
    B.φ′(x)dx
    C.f′(t)φ′(x)dt
    D.f′(t)dx

    答案：A
    解析：

  • 第2题：

    设函数y=esinx，求dy．


    答案：
    解析：
    解法1因为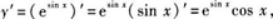
    则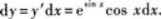

    解法2直接求微分：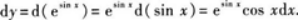

  • 第3题：

    若y=e2x，则dy=_________．


    答案：
    解析：
    【答案】2e2xdx【考情点拨】本题考查了微分的知识点．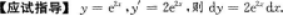

  • 第4题：

    设y=5+lnx，则dy=_______。


    答案：
    解析：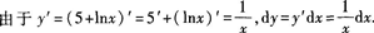

  • 第5题：

    设函数y=(x-3)4，则dy=__________．


    答案：
    解析：
    4(x-3)3dx

  • 第6题：

    设y=f（t），t=φ（x）都可微，则dy=（）。

    • A、f＇（t）dt
    • B、φ＇（x）dx
    • C、f＇（t）φ＇（x）dt
    • D、f＇（t）dx

    正确答案:A

  • 第7题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    1

    B

    2

    C

    3

    D

    4


    正确答案： B
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第8题：

    单选题
    设y=f（t），t=φ（x）都可微，则dy=（）。
    A

    f＇（t）dt

    B

    φ＇（x）dx

    C

    f＇（t）φ＇（x）dt

    D

    f＇（t）dx


    正确答案： D
    解析： 暂无解析

  • 第9题：

    单选题
    设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
    A

    （ln2－1）dx

    B

    （l－ln2）dx

    C

    （ln2－2）dx

    D

    ln2dx


    正确答案： C
    解析：
    2xy＝x＋y等式两边求微分，得2xyln2d（xy）＝dx＋dy，即2xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|x＝0＝（ln2－1）dx。

  • 第10题：

    填空题
    设函数y＝y（x）由方程y＝1－xey确定，则（dy/dx）|x＝0＝____。

    正确答案： -e
    解析：
    设F（x，y）＝y－1＋xey，则dy/dx＝－Fx′/Fy′＝－ey/（1＋xey）。x＝0时，y＝1，代入上式得（dy/dx）|x＝0＝－e。

  • 第11题：

    填空题
    设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝____。

    正确答案： (ln2-1)dx
    解析：
    2xy＝x＋y等式两边求微分，得2xyln2d（xy）＝dx＋dy，即2xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|x＝0＝（ln2－1）dx。

  • 第12题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    e


    正确答案： B
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第13题：

    设函数y=sinx2+2x，求dy．


    答案：
    解析：
    y'=2xcosx2+2，则dy=2xcosx2+2)dx．

  • 第14题：

    设函数y=x4sinx，求dy．


    答案：
    解析：
    因为y'=4x3sinx+x4cosx，所以dy=(4x3sinx+x4cosx)dx．

  • 第15题：

    设y=1n(cosx)，则微分dy等于:


    答案：C
    解析：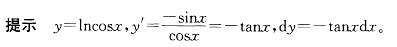

  • 第16题：

    设Y=sinx+COSx，则dy等于()．

    A.(cosx+sinx)dx
    B.(-cosx+sinx)dx
    C.(cosx-sinx)dx
    D.(-cosx-sinx)dx

    答案：C
    解析：
    由微分的基本公式及四则运算法则可得因此选C．

  • 第17题：

    设随机变量X，Y的期望与方差都存在， 则下列各式中成立的是（）

    • A、E（X+Y）=EX+EY
    • B、E（XY）=EX·EY
    • C、D（X+Y）=DX+XY
    • D、D（XY）=DX·DY

    正确答案:A

  • 第18题：

    填空题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

    正确答案： -1/7
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第19题：

    填空题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

    正确答案： 1
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第20题：

    填空题
    设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx____。

    正确答案： ln[(2x-1)/(x+1)]/(x+1)2
    解析：
    令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）2。dy/dx＝f′（u）·u′（x）＝ln（u1/3）·3/（x＋1）2＝ln[（2x－1）/（x＋1）]/（x＋1）2。

  • 第21题：

    填空题
    设y＝f（lnx）ef（x），其中f可微，则dy＝____。

    正确答案： [f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx
    解析：
    由y′＝f′（lnx）ef（x）/x＋f′（x）f（lnx）ef（x），得dy＝[f′（lnx）ef（x）/x＋f′（x）f（lnx）ef（x）]dx。

  • 第22题：

    单选题
    设y＝ln（cosx），则微分dy等于（　　）。[2012年真题]
    A

    dx/cosx

    B

    cotxdx

    C

    －tanxdx

    D

    －dx/（cosxsinx）


    正确答案： D
    解析：
    等式两边同时微分，得：dy＝f′（x）dx＝（－sinx）dx/cosx＝－tanxdx。

  • 第23题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    ln1

    B

    0

    C

    sin1

    D

    1


    正确答案： A
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

相关内容