设y=ln（cosx），则微分dy等于：

题目

相似考题

1.设函数y=1/(1+cosx)，则y′=__________。

2.设y=(1+x)1/x，则y‘(1)等于： A. 2 B. e C. 1、2-ln2 D. 1-ln4

3.设函数z=ln(x+y2)，则全微分dz=_______．

4.设y＝ln（sinx），则二阶导数y″等于（　　）。

更多“设y=ln（cosx），则微分dy等于： ”相关问题

第1题：

设y=x2cosx+2x+e，则y′=．

答案：
解析：
【答案】2xcosx-x2sinx+2xIn2【考情点拨】本题考查了一元函数的一阶导数的知识点．
【应试指导】(x2cosx)'=2xcosx-x2sinx，(2x)'=2x·In2，e'=0。所以y'=2xcosx-x2sinx+2xIn2．
第2题：

设函数y=ln(x2+1)，求dy．

答案：
解析：
第3题：

若函数z=ln(xy)/y,则当x=e,y=e-1时，全微分dz等于（）。

A. edx + dy B. e2dx-dy C. dx + e2dy D. edx+e2dy

答案：C
解析：
正确答案是C。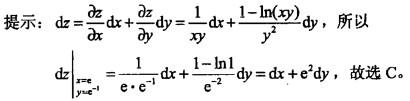
第4题：

设y=cosx，则y′′=( )

A.sinx
B.cosx
C.-cosx
D.-sinx

答案：C
解析：
【考情点拨】本题考查了函数的二阶导数的知识点.【应试指导】y=cosx，y'=-sinx，y''=-cosx.
第5题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
1
B
2
C
3
D
4

正确答案： B
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第6题：

单选题
设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（　　）。
A
y″－y′＋y＝0
B
y″－2y′＋2y＝0
C
y″－2y′＝0
D
y′＋2y＝0

正确答案： B
解析：
根据题中所给的通解y＝e^x（c₁sinx＋c₂cosx）的结构可知，所求方程对应的特征根为λ₁_，₂＝1±i，特征方程为[λ－（1＋i）][λ－（1－i）]＝λ²－2λ＋2＝0，则所求方程为y″－2y′＋2y＝0。
第7题：

单选题
设函数ψ（x）具有二阶连续导数，且ψ（0）＝ψ′（0）＝0，并已知yψ（x）dx＋[sinx－ψ′（x）]dy＝0是一个全微分方程，则ψ（x）等于（　　）。
A
（xsinx）/2
B
x³－x²/2
C
x²e^x
D
（xsinx）/2＋C₁cosx＋C₂sinx

正确答案： A
解析：
由于yψ（x）dx＋[sinx－ψ′（x）]dy＝0是一个全微分方程，则∂Q/∂x＝∂P/∂y，ψ″（x）＋ψ（x）＝cosx。从选项的结构中，可以看出，B、C项无正余弦，一定不是ψ″（x）＋ψ（x）＝cosx的特解，又因为（xsinx）/2＋C₁cosx＋C₂sinx中含有自由常数，故D项不是特解。将A项代入ψ″（x）＋ψ（x）＝cosx，等式两边相等，故A项是该方程特解。
第8题：

单选题
设方程x2＋y2＋z2＝4z确定可微函数z＝z（x，y），则全微分dz等于（　　）。[2014年真题]
A
（ydx＋xdy）/（2－z）
B
（xdx＋ydy）/（2－z）
C
（dx＋dy）/（2＋z）
D
（dx－dy）/（2－z）

正确答案： C
解析：
对等式两边分别同时求导，得：2xdx＋2ydy＋2zdz＝4dz。所以dz＝（xdx＋ydy）/（2－z）
第9题：

填空题
设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx____。

正确答案： ln[(2x-1)/(x+1)]/(x+1)²
解析：
令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）²。dy/dx＝f′（u）·u′（x）＝ln（u^1/3）·3/（x＋1）²＝ln[（2x－1）/（x＋1）]/（x＋1）²。
第10题：

单选题
设y＝ln（cosx），则微分dy等于（　　）。[2012年真题]
A
dx/cosx
B
cotxdx
C
－tanxdx
D
－dx/（cosxsinx）

正确答案： D
解析：
等式两边同时微分，得：dy＝f′（x）dx＝（－sinx）dx/cosx＝－tanxdx。
第11题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
ln1
B
0
C
sin1
D
1

正确答案： A
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第12题：

单选题
设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（　　）。
A
y″＋2y′＋2y＝0
B
y″－2y′＋2y＝0
C
y″－2y′－2y＝0
D
y″＋2y′＋2y＝0

正确答案： A
解析：
根据题中所给的通解y＝e^x（c₁sinx＋c₂cosx）的结构可知，所求方程对应的特征根为λ₁_，₂＝1±i，特征方程为[λ－（1＋i）][λ－（1－i）]＝λ²－2λ＋2＝0，则所求方程为y″－2y′＋2y＝0。
第13题：

设函数z=ln(x+y)，则全微分dz=________．

答案：
解析：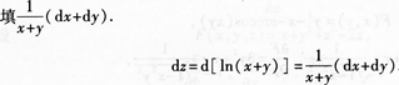
第14题：

设y=1n(cosx)，则微分dy等于:

答案：C
解析：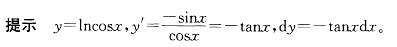
第15题：

设Y=sinx+COSx，则dy等于()．

A.(cosx+sinx)dx
B.(-cosx+sinx)dx
C.(cosx-sinx)dx
D.(-cosx-sinx)dx

答案：C
解析：
由微分的基本公式及四则运算法则可得因此选C．
第16题：

设，y=COSx，则y′等于()．

A.-sinx
B.sinx
C.-cosx
D.cosx

答案：A
解析：
由导数的基本公式可知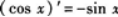，因此选A．
第17题：

填空题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

正确答案： 1
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第18题：

单选题
微分方程ydx＋（x－y）dy＝0的通解是（　　）。[2010年真题]
A
（x－y/2）y＝C
B
xy＝C（x－y/2）
C
xy＝C
D
y＝C/ln（x－y/2）

正确答案： D
解析：
微分方程ydx＋（x－y）dy＝0可写成ydx＋xdy＝ydy，右端仅含y，求积分得y²/2。左端既含x又含y，它不能逐项积分，但却可以化成d（xy），因此，直接求积分得到xy，从而便得到微分方程的隐式解：xy＝y²/2＋C，即（x－y/2）y＝C。
第19题：

单选题
设函数φ（x）具有二阶连续导数且φ（0）＝0，并且已知yφ（x）dx＋[sinx－φ（x）]dy＝0是一个全微分方程，则φ（x）＝（　　）。
A
－e^－^x/2＋（cosx）/2＋（sinx）/2
B
x³－x²/2＋1
C
x²e^x－2
D
（xcosx）/2＋C₁cosx＋C₂sinx

正确答案： D
解析：
由于yφ（x）dx＋[sinx－φ（x）]dy＝0是一个全微分方程，故∂Q/∂x＝∂P/∂y即cosx－φ′（x）＝φ（x）。即φ′（x）＋φ（x）＝cosx。解此一阶微分方程得φ（x）＝ce^－^x＋（cosx）/2＋（sinx）/2。又φ（0）＝0，代入上式得c＝－1/2，故φ（x）＝－e^－^x/2＋（cosx）/2＋（sinx）/2。
第20题：

单选题
下列函数中，可作为某二阶微分方程的通解的是（　　）。
A
y＝c₁x²＋c₂x＋c₃
B
x²＋y²＝c
C
y＝ln（c₁cosx）＋ln（c₂sinx）
D
y＝c₁sin²x＋c₂cos²x

正确答案： D
解析：
A项中，含有三个独立的任意常数，则A项为三阶微分方程的通解；B项中，含有一个独立的任意常数，则B项为一阶微分方程的通解；C项中，因为y＝ln（c₁cosx）＋ln（c₂sinx）＝ln|c₁|＋ln|c₂|＋ln|cosx|＋ln|sinx|＝c＋ln|cosx|＋ln|sinx|。故C项中含有一个独立的任意常数，则C项为一阶微分方程的通解。
第21题：

单选题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
A
（ln2－1）dx
B
（l－ln2）dx
C
（ln2－2）dx
D
ln2dx

正确答案： C
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。
第22题：

单选题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
A
ln2－1
B
（ln2－1）dx
C
ln2＋1
D
（ln2＋1）dx

正确答案： D
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。
第23题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
0
B
1
C
2
D
e

正确答案： B
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

itgle.com

设y=ln（cosx），则微分dy等于：

题目

相似考题

更多“设y=ln（cosx），则微分dy等于： ”相关问题

相关内容