设y=2^x，则dy等于()．A.x2x-1dx B.2x-1dx C.2xdx D.2xln2dx

题目

设y=2^x，则dy等于()．

A.x2x-1dx
B.2x-1dx
C.2xdx
D.2xln2dx

相似考题

1.设X~N(3,42),且Y=3X＋4,则DY等于()。A、27B、25C、144D、43

2.设y=ln（cosx），则微分dy等于：

3.设参数方程确定了y是x的函数，且f(t)存在，f(0) = 2， f(0) = 2，则当t=0时，dy/dx的值等于： A. 4/3 B. -4/3 C. -2 D. 2

4.设(X,Y)相互独立,EX=EY=0,DX=DY=1,则E(X＋Y＋1)^2=5。()此题为判断题(对，错)。

更多“设y=2^x，则dy等于()．”相关问题

第1题：

设函数y=sinx2+2x，求dy．

答案：
解析：
y'=2xcosx2+2，则dy=2xcosx2+2)dx．
第2题：

设函数y=ln(x2+1)，求dy．

答案：
解析：
第3题：

若函数z=ln(xy)/y,则当x=e,y=e-1时，全微分dz等于（）。

A. edx + dy B. e2dx-dy C. dx + e2dy D. edx+e2dy

答案：C
解析：
正确答案是C。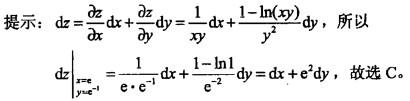
第4题：

设Y=e-3x，则dy等于()．

A.e-3xdx
B.-e-3xdx
C.-3e-3xdx
D.3e-3xdx

答案：C
解析：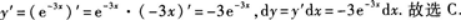
第5题：

设函数y=(x-3)4，则dy=__________．

答案：
解析：
4(x-3)3dx
第6题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
1
B
2
C
3
D
4

正确答案： B
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第7题：

填空题
设方程x＝yy确定y是x的函数，则dy＝____。

正确答案： dx/[x(1+lny)]
解析：
由dx＝d（y^y）＝d（e^ylny）＝y^yd（ylny）＝y^y（1＋lny）dy，得dy＝dx/[y^y（1＋lny）]＝dx/[x（1＋lny）]。
第8题：

单选题
设z＝φ（x2－y2），其中φ有连续导数，则函数z满足（　　）。
A
x∂z/∂x＋y∂z/∂y＝0
B
x∂z/∂x－y∂z/∂y＝0
C
y∂z/∂x＋x∂z/∂y＝0
D
y∂z/∂x－x∂z/∂y＝0

正确答案： D
解析：
令u＝x²－y²，则z＝φ（u），∂z/∂x＝φ′（u）·2x＝2xφ′（u），∂z/∂y＝－2yφ′（u），故y∂z/∂x＋x∂z/∂y＝0。
第9题：

单选题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
A
（ln2－1）dx
B
（l－ln2）dx
C
（ln2－2）dx
D
ln2dx

正确答案： C
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。
第10题：

填空题
设函数y＝y（x）由方程y＝1－xey确定，则（dy/dx）|x＝0＝____。

正确答案： -e
解析：
设F（x，y）＝y－1＋xe^y，则dy/dx＝－F_x′/F_y′＝－e^y/（1＋xe^y）。x＝0时，y＝1，代入上式得（dy/dx）|_x_＝₀＝－e。
第11题：

单选题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
A
ln2－1
B
（ln2－1）dx
C
ln2＋1
D
（ln2＋1）dx

正确答案： D
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。
第12题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
0
B
1
C
2
D
e

正确答案： B
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第13题：

设函数y=sin(x2-1)，则dy等于()．

A.cos(x2-1)dx
B.-cos(x2-1)dx
C.2xcos(x2-1)dx
D.-2xcos(x2-1)dx

答案：C
解析：
dy=y'dx=cos(x2-1)(x2-1)'dx=2xcos(x2-1)dx
第14题：

设y=1n(cosx)，则微分dy等于:

答案：C
解析：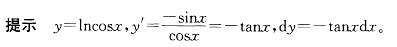
第15题：

设y=cos4x，则dy=（　　）

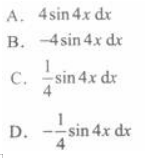答案：B
解析：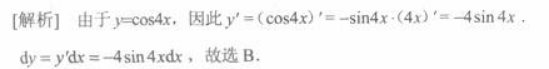
第16题：

设y=2x3，则dy=()．

A.2x2dx
B.6x2dx
C.3x2dx
D.x2dx

答案：B
解析：
由微分基本公式及四则运算法则可求得．也可以利用dy=y′dx求得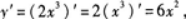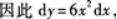故选B．
第17题：

填空题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

正确答案： -1/7
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。
第18题：

填空题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

正确答案： 1
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第19题：

单选题
设方程x2＋y2＋z2＝4z确定可微函数z＝z（x，y），则全微分dz等于（　　）。[2014年真题]
A
（ydx＋xdy）/（2－z）
B
（xdx＋ydy）/（2－z）
C
（dx＋dy）/（2＋z）
D
（dx－dy）/（2－z）

正确答案： C
解析：
对等式两边分别同时求导，得：2xdx＋2ydy＋2zdz＝4dz。所以dz＝（xdx＋ydy）/（2－z）
第20题：

填空题
设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx____。

正确答案： ln[(2x-1)/(x+1)]/(x+1)²
解析：
令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）²。dy/dx＝f′（u）·u′（x）＝ln（u^1/3）·3/（x＋1）²＝ln[（2x－1）/（x＋1）]/（x＋1）²。
第21题：

填空题
设y＝f（lnx）ef（x），其中f可微，则dy＝____。

正确答案： [f′(lnx)e^f⁽^x⁾/x+f′(x)f(lnx)e^f⁽^x⁾]dx
解析：
由y′＝f′（lnx）e^f^（^x^）/x＋f′（x）f（lnx）e^f^（^x^），得dy＝[f′（lnx）e^f^（^x^）/x＋f′（x）f（lnx）e^f^（^x^）]dx。
第22题：

填空题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝____。

正确答案： (ln2-1)dx
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。
第23题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
ln1
B
0
C
sin1
D
1

正确答案： A
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

itgle.com

设y=2^x，则dy等于()．A.x2x-1dx B.2x-1dx C.2xdx D.2xln2dx

题目

相似考题

更多“设y=2^x，则dy等于()．”相关问题

相关内容