itgle.com

函数f（x,y)在点（x,y)处偏导数存在是f（x,y)在点（x,y)处可微分的（）条件。A．充分B．必要C．充要;D．既非充分也非必要.

题目

函数f（x,y)在点（x,y)处偏导数存在是f（x,y)在点（x,y)处可微分的（）条件。

A．充分

B．必要

C．充要;

D．既非充分也非必要.

相似考题

1.以下结论正确的是()。A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.

2.函数z=f(x，y)在点(x0，y0)处连续是z=f(x，y)在点(x0，y0)处存在一阶偏导数的(58)。A．充分条件B．必要条件C．充要条件D．既非充分，又非必要条件

3.下列结论正确的是( ).A.x=f(x，y)在点(x，y)的偏导数存在是f(x，y)在该点连续的充分条件 B.z=f(x，y)在点(x，y)连续是f(x，y)的偏导数存在的必要条件 C.z=f(x，y)在点(x，y)的偏导数存在是f(x，y)在该点可微分的充分条件 D.z=(x，y)在点(x，y)连续是f(x，y)在该点可微分的必要条件

4.二元函数f(x,y)在点(x ,y)偏导数存在是f(x,y)在该点连续的()A、充分必要条件B、必要而非充分条件C、充分而非必要条件D、既非充分又非必要条件

更多“函数f（x,y)在点（x,y)处偏导数存在是f（x,y)在点（x,y)处可微分的（）条件。”相关问题

  • 第1题：

    函数f(x,y)在点P0(x0,y0)处有一阶偏导数是函数在该点连续的（　　）。

    A、必要条件
    B、充分条件
    C、充分必要条件
    D、既非充分又非必要条件

    答案：D
    解析：

  • 第2题：

    函数z=f(x，y)在点(x，y)处的偏导数存在是函数在该点可微的()

    A.必要条件
    B.充分条件
    C.既非必要又非充分条件
    D.充要条件

    答案：A
    解析：
    因为对于二元函数而言，在某点的偏导数存在，未必推出在该点可微，但是二元函数在某点可微，则在该点的偏导数一定存在，故应选A答案．

  • 第3题：

    设y=f（x）是（a，b）内的可导函数，x，x+△x是（a，b）内的任意两点，则：

    A. △y=f’（x）△x
    B.在x，x+△x之间恰好有一点ξ，使△y=f’（ξ）△x
    C.在x，x+△x之间至少存在一点ξ，使△y=f’（ξ）△x
    D.在x，x+△x之间的任意一点ξ，使△y=f’（ξ）△x

    答案：C
    解析：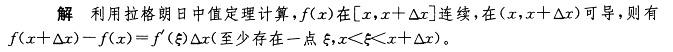

  • 第4题：

    若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是（ ）。
    A. f(x,y)的极值点一定是f(x,y)的驻点
    B.如果P0是f(x,y)的极值点，则P0点处B2-AC)
    C.如果P0是可微函数f(x,y)的极值点，则P0点处df=0
    D.f(x,y)的最大值点一定是f(x,y)的极大值点


    答案：C
    解析：
    提示：如果P0是可微函数f(x,y)的极值点，由极值存在必要条件，在P0点处有

  • 第5题：

    若z=f（x，y）在点（x0，y0）处可微，则在点（x0，y0）处，下列结论不正确的是（）

    • A、连续
    • B、偏导数存在
    • C、偏导数连续
    • D、切平面存在

    正确答案:C

  • 第6题：

    z=f（x，y）在P0（x0，y0）一阶偏导数存在是该函数在此点可微的什么条件（）？

    • A、必要条件
    • B、充分条件
    • C、充要条件
    • D、无关条件

    正确答案:A

  • 第7题：

    若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。

    • A、f（x，y）的极值点一定是f（x，y）的驻点
    • B、如果P0是f（x，y）的极值点，则P0点处B2-AC<0
    • C、如果P0是可微函数f（x，y）的极值点，则P0点处df=0
    • D、f（x，y）的最大值点一定是f（x，y）的极大值点

    正确答案:C

  • 第8题：

    下列结论不正确的是（）。

    • A、y=f（x）在点x0处可微，则f（x）在点x0处连续
    • B、y=f（x）在点x0处可微，则f（x）在点x0处可导
    • C、y=f（x）在点x0处连续，则f（x）在点x0处可微
    • D、y=f（x）在点x0处可导，则f（x）在点x0处连续

    正确答案:C

  • 第9题：

    单选题
    以下关于二元函数的连续性的说法正确是（　　）。
    A

    若f（x，y）沿任意直线y＝kx在点x＝0处连续，则f（x，y）在（0，0）点连续

    B

    若f（x，y）在点（x0，y0）点连续，则f（x0，y）在y0点连续，f（x，y0）在x0点连续

    C

    若f（x，y）在点（x0，y0）点处偏导数fx′（x0，y0）及fy′（x0，y0）存在，则f（x，y）在（x0，y0）处连续

    D

    以上说法都不对


    正确答案： C
    解析：
    根据二元函数f（x，y）在（x0，y0）出连续的定义可知B项正确。

  • 第10题：

    单选题
    考虑二元函数f（x，y）的下面4条性质：①f（x，y）在点（x0，y0）处连续；②f（x，y）在点（x0，y0）处的两个偏导数连续；③f（x，y）在点（x0，y0）处可微；④f（x，y）在点（x0，y0）处的两个偏导数存在。若用“P⇒Q”表示可由性质P推出Q，则有（　　）。
    A

    ②⇒③⇒①

    B

    ③⇒②⇒①

    C

    ③⇒④⇒①

    D

    ③⇒①⇒④


    正确答案： C
    解析：
    根据二元函数连续、可微及可导的关系可知②⇒③⇒①、②⇒③⇒④。

  • 第11题：

    单选题
    若z=f（x，y）在点（x0，y0）处可微，则在点（x0，y0）处，下列结论不正确的是（）
    A

    连续

    B

    偏导数存在

    C

    偏导数连续

    D

    切平面存在


    正确答案： C
    解析： 由可微一定连续，可微一定存在偏导数知（A）、（B）正确，由偏导数存在知切平面存在，（D）正确。但可微不一定偏导数连续，（C）不正确

  • 第12题：

    单选题
    下列结论正确的是（）.
    A

    x=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点连续的充分条件

    B

    z=f（x，y）在点（x，y）连续是f（x，y）的偏导数存在的必要条件

    C

    z=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点可微分的充分条件

    D

    z=（x，y）在点（x，y）连续是f（x，y）在该点可微分的必要条件


    正确答案： B
    解析： 暂无解析

  • 第13题：

    函数f（x，y）在点P0（x0，y0）处的一阶偏导数存在是该函数在此点可微分的（　　）。

    A． 必要条件
    B． 充分条件
    C． 充分必要条件
    D． 既非充分条件也非必要条件

    答案：A
    解析：
    函数f（x，y）在P0（x0，y0）可微，则f（x，y）在P0（x0，y0）的偏导数一定存在。反之，偏导数存在不一定能推出函数在该点可微。举例如下：
    函数



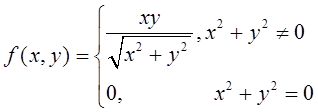
    在点（0，0）处有fx（0，0）＝0，fy（0，0）＝0，但函数f（x，y）在（0，0）处不可微。因此，函数f（x，y）在点P0（x0，y0）处的一阶偏导数存在是该函数在此点可微分的必要条件。

  • 第14题：

    设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.


    答案：1、2(ln2-1)
    解析：

  • 第15题：

    在点x＝0处的导数等于零的函数是（　　）

    A.y＝sinx
    B.y＝x－1
    C.y＝ex－x
    D.y＝x2－x

    答案：C
    解析：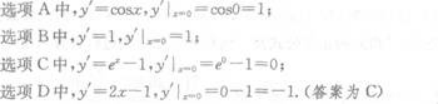

  • 第16题：

    若z=f(x,y)在（x0,y0）处的两个一阶偏导数存在，则函数z=f(x,y)在(x0,y0)处可微


    正确答案:错误

  • 第17题：

    对于二元函数z=f（x，y），在点（x0，y0）处连续是它在该点处偏导数存在的什么条件（）？

    • A、必要条件而非充分条件
    • B、充分条件而非必要条件
    • C、充分必要条件
    • D、既非充分又非必要条件

    正确答案:D

  • 第18题：

    下列结论不正确的是（）。

    • A、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处连续
    • B、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处可导
    • C、z=f（x，y）在点（x0，y0）处可导，则f（x，y）在点（x0，y0）处可微
    • D、z=f（x，y）在点（x0，y0）处偏导数连续，则f（x，y）在点（x0，y0）处连续

    正确答案:C

  • 第19题：

    下列结论正确的是（）.

    • A、x=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点连续的充分条件
    • B、z=f（x，y）在点（x，y）连续是f（x，y）的偏导数存在的必要条件
    • C、z=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点可微分的充分条件
    • D、z=（x，y）在点（x，y）连续是f（x，y）在该点可微分的必要条件

    正确答案:D

  • 第20题：

    下列结论正确的是（）．

    • A、z=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点连续的充分条件
    • B、z=f（x，y）在点（x，y）连续是f（x，y）的偏导数存在的必要条件
    • C、z=（x，y）在点（x，y）的偏导数存在是f（x，y）在该点可微分的充分条件
    • D、z=（x，y）在点（x，y）连续是f（x，y）在该点可微分的必要条件

    正确答案:D

  • 第21题：

    判断题
    若z=f(x,y)在（x0,y0）处的两个一阶偏导数存在，则函数z=f(x,y)在(x0,y0)处可微
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第22题：

    单选题
    二元函数z＝f（x，y）在点（x0，y0）处存在一阶连续偏导数是它在此点处可微的（　　）。
    A

    充分条件

    B

    必要条件

    C

    充要条件

    D

    以上都不是


    正确答案： C
    解析：
    一阶偏导数在（x0，y0）点连续，则函数在（x0，y0）处可微；而函数在（x0，y0）处可微，其一阶偏导数不一定连续。

  • 第23题：

    单选题
    可微函数f（x，y）在点（x0，y0）取得极小值，下列结论正确的是（　　）。
    A

    f（x0，y）在y＝y0处的导数等于零

    B

    f（x0，y）在y＝y0处的导数大于零

    C

    f（x0，y）在y＝y0处的导数小于零

    D

    f（x0，y）在y＝y0处的导数不存在


    正确答案： C
    解析：
    由题意可知，fx′（x0，y0）＝fy′（x0，y0）＝0。则当x＝x0时，f（x0，y）是一元可导函数，且它在y＝y0处取得极小值。故f（x0，y）在y＝y0处的导数为0。

  • 第24题：

    单选题
    若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。
    A

    f（x，y）的极值点一定是f（x，y）的驻点

    B

    如果P0是f（x，y）的极值点，则P0点处B2-AC<0

    C

    如果P0是可微函数f（x，y）的极值点，则P0点处df=0

    D

    f（x，y）的最大值点一定是f（x，y）的极大值点


    正确答案： C
    解析： 暂无解析

相关内容