itgle.com
单选题设f是由群到群的同态映射，则Ker（f）是（ ）。A G`的子群B G的子群C 包含G`D 包含G
题目
G`的子群
G的子群
包含G`
包含G
相似考题
更多“单选题设f是由群到群的同态映射，则Ker（f）是（ ）。A G`的子群B G的子群C 包含G`D 包含G”相关问题
-
第1题：
设G,*是6阶群，H是G的非平凡子群，则H,*的阶数可能是()。
A、1
B、3
C、4
D、5
参考答案：B
-
第2题：
设f(0)=g(0),且当x30时,f'(x)>g'(x),则当x>0时有()。A.f(x)
B.f(x)>g(x)
C.f(x)=g(x)
D.以上都不对
正确答案：B
-
第3题：
有限群G的阶为n，H是G的子群，则H的阶必除尽G的阶。()
参考答案：正确
-
第4题：
设int f (int)；和int g(int)；是函数f和g的原形，以下将f作为语句调用的是______ 。
A．g(f(3))
B．f(g(3))；
C．g(f(3)+2)；
D．p=f(g (3)+1)；
正确答案：D
解析：p=f(g(3)+1)：函数f被作为一个语句调用。 -
第5题：
f(x)与g(x)的图像如图所示，设u(x)=f[g(x)],则
答案：解析：
-
第6题：
设函数f（x），g（x）是大于零的可导函数，且f′（x）g（x）-f（x）g′（x）＜0，则当a＜x＜b时有（ ）《》（ ）A.f（x）g（b）＞f（b）g（x）
B.f（x）g（a）＞f（a）g（x）
C.f（x）g（x）＞f（b）g（b）
D.f（x）g（x）＞f（a）g（a）答案：A解析：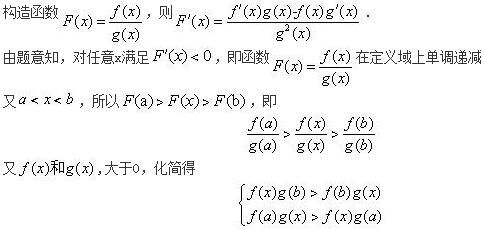
-
第7题：
在关系模式R（U，F）中，被F所逻辑蕴涵的函数依赖的全体称作F的（），记为（）。 设F和G是两个函数依赖集，如果F+包含于G+和G+包含于F+同时成立，即F+＝G+，则称F和G（）。
正确答案:闭包；F+；等价 -
第8题：
设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。
- A、F（x）+C也是f（x）的原函数，C为任意常数
- B、F（x）=G（x）+C，C为任意常数
- C、F（x）=G（x）+C，C为某个常数
- D、F’（x）=G’（x）
正确答案:B -
第9题：
单选题设函数f（x），g（x）在[a，b]上均可导（a＜b），且恒正，若f′（x）g（x）＋f（x）g′（x）＞0，则当x∈（a，b）时，下列不等式中成立的是（ ）。[2018年真题]Af（x）/g（x）＞f（a）/g（b）
Bf（x）/g（x）＞f（b）/g（b）
Cf（x）g（x）＞f（a）g（a）
Df（x）g（x）＞f（b）g（b）
正确答案： C解析：
因为[f（x）g（x）]′＝f′（x）g（x）＋f（x）g′（x）＞0，所以函数f（x）g（x）在[a，b]上单调递增。所以，当x∈（a，b）时，f（a）g（a）＜f（x）g（x）＜f（b）g（b）。 -
第10题：
单选题设f是由群到群的同态映射，则Ker（f）是（ ）。AG`的子群
BG的子群
C包含G`
D包含G
正确答案： C解析：
同态的核定义为Ker（f）＝{g∈G：f（g）＝1`}。因为：
①f（1）＝1`，所以1∈Ker（f）；
②若g1，g2∈Ker（f），那么f（g1×g2）＝f（g1）*f（g2）＝1`*1`＝1`，则g1×g2∈Ker（f）；
③若g∈Ker（f），即f（g）＝1`，那么1`＝f（1）＝f（g－1×g）＝f（g－1）*f（g）＝f（g－1）*1`，所以f（g－1）＝1`，即g－1∈Ker（f）。
上面三点说明ker（f）是G的子群，故本题选B。 -
第11题：
填空题在关系模式R（U，F）中，被F所逻辑蕴涵的函数依赖的全体称作F的（），记为（）。 设F和G是两个函数依赖集，如果F+包含于G+和G+包含于F+同时成立，即F+＝G+，则称F和G（）。正确答案： 闭包,F+,等价解析： 暂无解析 -
第12题：
单选题设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（ ）。[2018年真题]Af[g（x）]
Bf[f（x）]
Cg[f（x）]
Dg[g（x）]
正确答案： B解析：
D项，令T（x）＝g[g（x）]。因为T（－x）＝g[g（－x）]＝g[－g（x）]＝－g[g（x）]，所以T（－x）＝－T（x），所以g[g（x）]为奇函数。 -
第13题：
设函数f(x)为奇函数,g(x)为偶函数,则复合函数()是奇函数。A.f(f(x))
B.g(f(x))
C.f(g(x))
D.g(g(x))
正确答案：A
-
第14题：
设群G是阶为n的有限群，则群G的所有元素的阶都不超过n。()
参考答案：正确
-
第15题：
设f(x)，g(x)ϵP[x J. 若f(x)lg(x)，g(x)lf(x)，则 f(x)与g(x)的关系是( ).
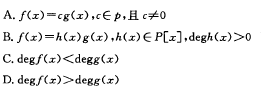参考答案：A
-
第16题：
设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（ ）。A． f[g（x）]
B． f[f（x）]
C． g[f（x）]
D． g[g（x）]答案：D解析：D项，令T（x）＝g[g（x）]。因为T（－x）＝g[g（－x）]＝g[－g（x）]＝－g[g（x）]，所以T（－x）＝－T（x），所以g[g（x）]为奇函数。 -
第17题：
设函数f（x），g（x）在[a，b]上均可导（a＜b），且恒正，若f′（x）g（x）＋f（x）g′（x）＞0，则当x∈（a，b）时，下列不等式中成立的是（ ）。A． [f（x）/g（x）]＞[f（a）/g（b）]
B． [f（x）/g（x）]＞[f（b）/g（b）]
C． f（x）g（x）＞f（a）g（a）
D． f（x）g（x）＞f（b）g（b）答案：C解析：因为[f（x）g（x）]′＝f′（x）g（x）＋f（x）g′（x）＞0，所以函数f（x）g（x）在[a，b]上单调递增。所以，当x∈（a，b）时，f（a）g（a）＜f（x）g（x）＜f（b）g（b）。 -
第18题：
设f（x）和g（x）在（-∞，+∞）内可导，且f（x）＜g（x），则必有（ ）《》（ ）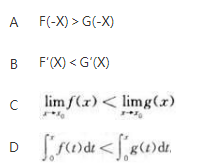
答案：C解析：
-
第19题：
设F和G是两个函数依赖集，如果F+包含于G+和G+包含于F+同时成立，即F+＝G+，则称F和G（）
正确答案:等价 -
第20题：
设K是个数域，K[x]中的多项式f（x），g（x），若有f=g，则可以得到什么？（）
- A、f（x）=g（f（x））
- B、g（x）=f（f（x））
- C、f（x）=g（x）
- D、g（x）=f（g（x））
正确答案:C -
第21题：
填空题设F和G是两个函数依赖集，如果F+包含于G+和G+包含于F+同时成立，即F+＝G+，则称F和G（）正确答案： 等价解析： 暂无解析 -
第22题：
单选题设K是个数域，K[x]中的多项式f（x），g（x），若有f=g，则可以得到什么？（）Af（x）=g（f（x））
Bg（x）=f（f（x））
Cf（x）=g（x）
Dg（x）=f（g（x））
正确答案： C解析： 暂无解析 -
第23题：
问答题设函数f（x），g（x）二次可导，满足函数方程f（x）g（x）＝1，又f′（x）≠0，g′（x）≠0，则f″（x）/f′（x）－f′（x）/f（x）＝g″（x）/g′（x）－g′（x）/g（x）。正确答案：
f(x)g(x)=1,则f′(x)g(x)+f(x)g′(x)=0①
即f′(x)/f(x)=-g′(x)/g(x)②
对①两边求导得f″(x)g(x)+2f′(x)g′(x)+f(x)g″(x)=0,即f″(x)+2f′(x)g′(x)/g(x)+f(x)g″(x)/g(x)=0,即f″(x)/f′(x)+2f′(x)g′(x)/f′(x)g(x)+f(x)g″(x)/f′(x)g(x)=0。
由①得f″(x)/f′(x)+2g′(x)/g(x)-f(x)g″(x)/f(x)g′(x)=0,则f″(x)/f′(x)+2g′(x)/g(x)=g″(x)/g′(x)。
又由②得f″(x)/f′(x)-f′(x)/f(x)=g″(x)/g′(x)-g′(x)/g(x)。解析： 暂无解析 -
第24题：
单选题设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（）。Af[g(x)]
Bf[f(x)]
Cg[f(x)]
Dg[g(x)]
正确答案： D解析：