itgle.com

设f(x)=3x,g(x)=x2，则函数g[f(x)]-f[g(x)]=_______________.

题目

设f(x)=3x,g(x)=x2，则函数g[f(x)]-f[g(x)]=_______________.

相似考题

1.设函数f(x)=lnx，g(x)=e2x+1，则f[g(x)]=______。

2.设f (x)=x2,g(x)=ex,则f [g(x)]=_________.

3.设函数f(x)为奇函数,g(x)为偶函数,则复合函数()是奇函数。A.f(f(x))B.g(f(x))C.f(g(x))D.g(g(x))

4.设f(x),g(x),h(x)均为奇函数,则()中所给定的函数是偶函数。A、f(x)g(x)h(x)B、[f(x)+g(x)]h(x)C、f(x)+g(x)D、f(x)+g(x)+h(x)

参考答案和解析
正确答案：
更多“设f(x)=3x,g(x)=x2,则函数g[f(x)]－f[g(x)]=_______________. ”相关问题

  • 第1题：

    设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（　　）。

    A． f[g（x）]
    B． f[f（x）]
    C． g[f（x）]
    D． g[g（x）]

    答案：D
    解析：
    D项，令T（x）＝g[g（x）]。因为T（－x）＝g[g（－x）]＝g[－g（x）]＝－g[g（x）]，所以T（－x）＝－T（x），所以g[g（x）]为奇函数。

  • 第2题：

    设函数f（x），g（x）是大于零的可导函数，且f′（x）g（x）-f（x）g′（x）＜0，则当a＜x＜b时有（ ）《》（ ）

    A.f（x）g（b）＞f（b）g（x）
    B.f（x）g（a）＞f（a）g（x）
    C.f（x）g（x）＞f（b）g（b）
    D.f（x）g（x）＞f（a）g（a）

    答案：A
    解析：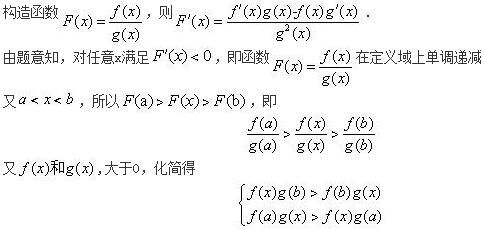

  • 第3题：

    设f（x) g（x)是恒大于零的可导函数，且f’（x)g（x) - f（x) g’（x) ＜ 0,则当a＜x ＜b时，有

    A．f(x)g(b) ＞ f(b)g(x)

    B．f(x)g(a) ＞ f(a)g(x)

    C．f(x)g(x) ＞ f(b)g(b)

    D．f(x)g(x) ＞ f(a)g(a)


    故应选(A)．

  • 第4题：

    设函数f（x），g（x）在[a，b]上均可导（a＜b），且恒正，若f′（x）g（x）＋f（x）g′（x）＞0，则当x∈（a，b）时，下列不等式中成立的是（　　）。

    A． [f（x）/g（x）]＞[f（a）/g（b）]
    B． [f（x）/g（x）]＞[f（b）/g（b）]
    C． f（x）g（x）＞f（a）g（a）
    D． f（x）g（x）＞f（b）g（b）

    答案：C
    解析：
    因为[f（x）g（x）]′＝f′（x）g（x）＋f（x）g′（x）＞0，所以函数f（x）g（x）在[a，b]上单调递增。所以，当x∈（a，b）时，f（a）g（a）＜f（x）g（x）＜f（b）g（b）。

  • 第5题：

    设函数f （x)=x2，g （x)=2x，则

    A．f (x)是g (x)的一个原函数

    B．g (x)是f (x)的一个原函数

    C．f (x)与g (x)是同一个函数的原函数

    D．f (x)与g (x)有相同的原函数


    F（x）=G（x）+C，C为任意常数

相关内容