itgle.com

如图所示，矩形ABCD的面积为1,E、F、G、H分别为四条边的中点，FI的长度是IE的两倍，问阴影部分的面积为多少？

题目
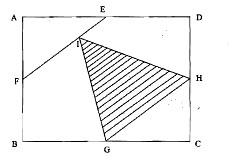
如图所示，矩形ABCD的面积为1,E、F、G、H分别为四条边的中点，FI的长度是IE的两倍，问阴影部分的面积为多少？



相似考题

1.如下图所示，X、Y、Z分别是面积为64、180、160的三张不同开关的纸片。它们部分重叠放在一起盖在桌面上，总共盖住的面积为209。且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。问阴影部分的面积是多少？A15 B16C14 D18

2.如图，正四面体P-ABC的棱长为a，D、E、F分别为PA、PB、PC的中点，G、H、M 分别为DE，EF，FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为（ ）。A. 1 : 8 B. 1 : 16 C. 1 : 32 D. 1 : 64

3.如图，长方形ABCD的两条边长分别为8m和6m，四边形OEFG的面积是4m2，则阴影部分的面积为（）。A.32m2 B.28m2 C.24m2 D.20m2

4.如右图，正四面体P-ABC的棱长为口，D、E、F分别为棱PA、PB、PC的中点，G、H、M分别为DE、EF、FD的中点，则三角形GHM的面积与正四面体P-ABC的表面积之比为：A.1：8B.1：16C.1：32D.1：64

更多“如图所示，矩形ABCD的面积为1,E、F、G、H分别为四条边的中点，FI的长度是IE的两倍，问阴影部分的面积为多少？ ”相关问题

  • 第1题：

    长方形ABCD的面积是72平方厘米，E、F分别是CD，BC的中点。问三角形的面积为多少平方厘米？

    A.24
    B.27
    C.36
    D.40


    答案：B
    解析：

  • 第2题：

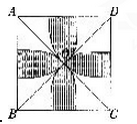
    在边长为1的正方形ABCD中，AC与BD相交于O，以A、B、C、D分别为圆心，以对角线长的一半为半径画圆弧与正方形的边相交，如图，则图中阴影部分的面积为多少?(π=3．14)


    A.0．43
    B.0．57
    C.0．64
    D.0．71

    答案：C
    解析：

  • 第3题：

    使用估算模式计算面源影响时，需要下列哪些面源参数? ( )
    A. 宽度 (m) (矩形面源较短的一边)
    B. 面源排放速率 [g/ (s. m2 ) ]
    C. 排放高度 (m)
    D. 计算点的高度
    E. 长度 (m)( 矩形面源较长的一边)


    答案：A,B,C,E
    解析：
    选项D不属于面源参数，属于预测点的参数。

  • 第4题：

    把一个正方形的四个角分别切除一个等腰三角形，剩下一个长宽不等的矩形。若被切除部分的总面积为400平方厘米，且切除的三角形的直角边的长度均为整数，则所剩矩形的面积为（ ）平方厘米。

    A. 320
    B. 336
    C. 360
    D. 384
    E. 400
    F. 420
    G. 441
    H. 464

    答案：D
    解析：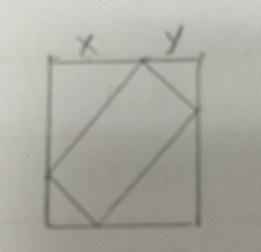

  • 第5题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )
    A. 11.75 B. 16.45 C. 19.625 D. 39. 25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10x10x2，所以大半圆的面积是1/2x1/4xπx10x10x2=25π（平方厘米）；
    小半圆的面积是π/2X5X5 = 12. 5π（平方厘米）；
    阴影的面积是25π-12. 5π=12. 5π=39. 25（平方厘米）。
    故本题选D。

  • 第6题：

    如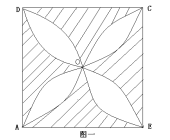，四边形ABCD是边长为1的正方形，弧AOB，BOC，COD，DOA均为半圆，则阴影部分的面积为



    答案：E
    解析：

  • 第7题：

    在右图的长方形中，长和宽分别是6cm和4cm，阴影部分的面积和是10cm2，求四边形ABCD的面积为多少平方厘米？（ ）
    A. 2 B. 4
    C. 5 D. 8


    答案：B
    解析：
    SΔAGF=4X6/2=12(cm2)，它与阴影部分的面积和是12 + 10 = 22(cm2)，而五边形HCEFG的面积是长方形HEFG的3/4，即4X6x3/4 = 18(cm2)，所以四边形ABCD的面积是22 - 18 =4 (cm2)。

  • 第8题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )

    A. 11.75 B. 16.45 C. 19.625 D. 39.25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。
    由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10X10X2，所以大半圆的面积是1/2x1/4xπx10x10x2 = 25π(平方厘米)；
    小半圆的面积是1/2πx5x5 = 12. 5π(平方厘米)；
    阴影的面积是25π-12. 5π=12. 5π=39. 25(平方厘米)。
    故本題选D。

  • 第9题：

    如图，已知四棱锥P-ABCD底面ABCD为矩形，侧棱PA⊥ABCD，AB=AP=21/2AD=2，E，F分别为PC，AB的中点。
    (I)证明：EF∥面PAD。
    (II)求三棱锥B-PFC的体积。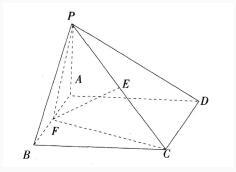


    答案：
    解析：

  • 第10题：

    如图，正方体ABCD-A1B1C1D1中，E，F，G分别为AA1，A1D1，BC的中点，则异面直线EF与D1G所成角的大小为__________。



    答案：
    解析：
    连接AD1，AG，由于EF平行于AD1，则异面直线EF与D1G所成角等于AD1与D1G所成角。设正方体棱长为2，在△AD1G中，D1G=3，根据余弦定理，cos∠AD1G=

  • 第11题：

    使用估算模式计算面源影响时，需要下列哪些面源参数？（）

    • A、宽度（m）（矩形面源较短的一边）
    • B、面源排放速率[g/（s.m2）]
    • C、排放高度（m）
    • D、计算点的高度
    • E、长度（m）（矩形面源较长的一边）

    正确答案:A,B,C,E

  • 第12题：

    多选题
    使用估算模式计算面源影响时，需要下列哪些面源参数？（）
    A

    宽度（m）（矩形面源较短的一边）

    B

    面源排放速率[g/（s.m2）]

    C

    排放高度（m）

    D

    计算点的高度

    E

    长度（m）（矩形面源较长的一边）


    正确答案： E,C
    解析： 选项D不属于面源参数，属于预测点的参数。

  • 第13题：

    如图所示，矩形ABCD的面积为1，E、F、G、H分别为四条边的A 中点，FI的长度是IE的两倍，问阴影部分的面积为多 少？（ ）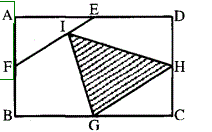



    答案：B
    解析：
    这个题目需要做辅助线，连接FG、EH。
    因为E、F、G、H分别为四条边的中点，则平行四边形EFGH的面积是矩形ABCD面积的 1/2，而三角形IGH的面积是平行四边EFGH面积的1/2，所以阴影部分的面积为1/4。

  • 第14题：

    如图所示，X、Y、Z分别是面积为64、180、160的三张不同形状的纸片。它们部分重叠放在一起盖在桌面上，总共盖住的面积为290。且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36。问阴影部分的面积是多少?（）[银行真题]

    A.15
    B.16
    C.14
    D.18


    答案：B
    解析：
    根据三个集合的容斥公式，阴影部分的面积为290+24+70+36-(64+180+160)=16。

  • 第15题：

    将棱长为1的正方体的六个面的中点相连接可以得到一个八面体，则这个八面体的体积为：


    答案：A
    解析：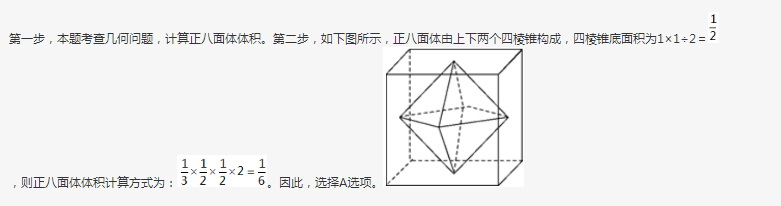

  • 第16题：

    连接正四面体侧棱的中点和底面的中心A、E、F、G、H构成多面体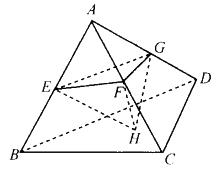

    （如右图所示）。问该多面体与正四面体的体积比是多少？（ ）

    A. 1 : 8
    B. 1 : 6
    C. 1：4
    D. 1 : 2

    答案：C
    解析：
    如图所示，AEFG与ABCD的边长比为1：2，所以二者的面积比为1 : 4。又因为正四面体A—EFG与正四面体A—BCD高的比为1 : 2，所以，正四面体A—EFG与正四面体A—BCD的体积比为1 : 8，所以该多面体与正四面体A—BCD的体积比为2 : 8，即1 : 4。故本题答案为C。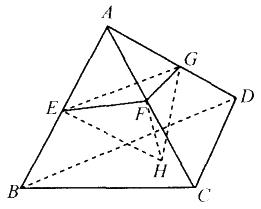

  • 第17题：

    长方形A BCD的面积是72平方厘米，E、F分别是CD、BC的中点。问三角形的面积为多少平方厘米？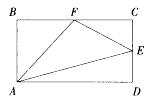


    A.24
    B.27
    C.36
    D.40

    答案：B
    解析：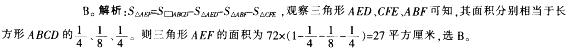

  • 第18题：

    如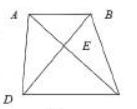，在四边形ABCD中，AB//CD，AB与CD的边长分别为4和8，若ABE的面积为4，则四边形ABCD的面积为（ ）

    A.24
    B.30
    C.32
    D.36
    E.40

    答案：D
    解析：

  • 第19题：

    一块种植花卉的矩形土地如图所示，AD边长是AB的2倍，E为CD边的中点，甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。问种植白花的面积占矩形土地面积的：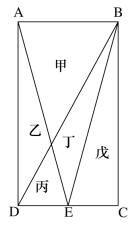



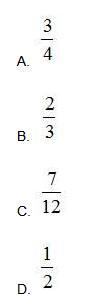    答案：C
    解析：
    赋值丙面积为1；则甲面积为4（相似图形，面积比等于边长平方比）；乙和丁面积为2（等高情况下，三角形面积比等于底边长比）；戊的面积与丙丁面积之和相等，面积为3；总面积为12，其中种白花的面积为7，因此占比为7/12。正确答案为C。

  • 第20题：

    如图，平行四边形ABCD的面积是54平方厘米，点E、F、G分别是平行四边形ABCD边上的中点，H为AD边上的任意一点，则阴影部分的面积为（ ）平方厘米。


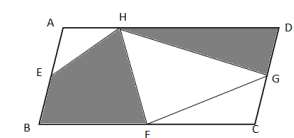    A. 27
    B. 28
    C. 32
    D. 36

    答案：A
    解析：
    方法一：如图所示，由于H为AD边上的任意一点，假设H点与A点重叠，则左边阴影为三角形ABF，其面积为三角形ABC的一半；右边阴影为三角形ADG，其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半，平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。



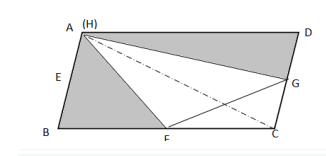
    方法二：如图所示，连接BH和CH，由于点E、F、G分别是平行四边形ABCD边上的中点，则三角形AEH和BEH相等，三角形BFH和CFH相等，三角形CGH和DGH相等，因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。

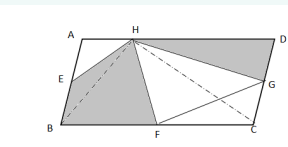
  • 第21题：

    如图，四棱锥S-ABCD的底面是矩形，SA⊥底面ABCD，P是BC边的中点，AD=2，SA=AB=1。



    (1)求证：PD⊥平面SAP；
    (2)求三棱锥S-APD的体积。


    答案：
    解析：
    (1)证明：易知在△APD中，，AD=2，满足勾股定理，故PD⊥AP。SA⊥底面ABCD，则SA⊥PD。PD同时垂直于平面SAP内的两条相交直线，PD⊥平面SAP。 (2)

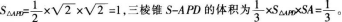
  • 第22题：

    作横截面为矩形，周长为80cm，高为30cm的容器，问容器的最大容积为多少？若油的密度为0.8g/cm3 ，求能装多少公斤的油？


    正确答案: 设该矩形的长为xcm，则宽为（40-x）cm 
    该矩形面积为：S=x（40-x）=-（x2-40x） 
    =-（x-20）2+400（cm2） 
    当x=20cm时，Smax=400cm2 
    则Vmax= Smax×30=12000（cm3） 
    油的重量G=ρV=0.8×12000=9600（g）=9.6kg 
    答：该容器的最大容积为12000cm3，能装9.6kg油。

  • 第23题：

    问答题
    作横截面为矩形，周长为80cm，高为30cm的容器，问容器的最大容积为多少？若油的密度为0.8g／cm3，求能装多少公斤的油？

    正确答案： 设该矩形长为xcm，则宽为（40－x）cm
    该矩形面积为：S＝x（40－x）＝－（x2－40x）＝－（x－20）2＋400（cm2）
    当x＝20cm时，Smax＝400cm2
    则Vmax＝Smax30＝400×30＝12000（cm3）
    油的重量G＝ρV＝0.8×12000＝9600（g）＝9.6kg
    答：该容器的最大容积为12000cm3，能装9.6kg的油。
    解析： 暂无解析

相关内容