假设某消费者的均衡如图所示。其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为消费者的无差异曲线,E点为效用最大化的均衡点已知商品1的价格P1=2元。(1)求消费者的收入;(2)求商品2的价格P2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E点的MRS12的值。
题目
假设某消费者的均衡如图所示。其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U为消费者的无差异曲线,E点为效用最大化的均衡点已知商品1的价格P1=2元。
(1)求消费者的收入;
(2)求商品2的价格P2;
(3)写出预算线方程;
(4)求预算线的斜率;
(5)求E点的MRS12的值。
相似考题
更多“假设某消费者的均衡如图所示。其中,横轴OX1和纵轴OX2分别表示商品1和商品2的数量,线段AB为消费者 ”相关问题
-
第1题:
假设一个消费者的效用函数为u= xy+y,其中z和y分别表示两种商品。 (1)请问此效用函数是拟凹的吗? (2)计算均衡需求函数和马歇尔需求函数。 (3)计算间接效用函数和支出函数。答案:解析:(1)该效用函数是拟凹函数。分析如下: 由消费者的效用函数可得商品z和y的边际效用分别为: MU=y,MUy=x+1 因此,边际替代率为: MRS=MUx/MUy=y/x+1 可以看出,边际替代率MRS随着x的增加而减少,因此该函数是拟凹函数。 (2)假设消费者的收入为I,则消费者的效用最大化问题为: max u=xy+y s.t. P1x+P2Y=I 其中,Pl和P2分别为x和y的价格。构造拉格朗日辅助函数L=ry+y-λ(P1x+P2Y-I),效 用最大化的一阶条件为:
解得: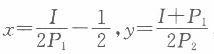
此即为x、y的马歇尔需求函数。 (3)间接效用函数和支出函数: 将最优解代人效用函数可得间接效用函数为: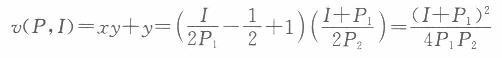
即间接效用函数为
支出函数与间接效用函数互为反函数,因此支出函数为:
-
第2题:
假设某商品需求函数为Q=100-2P,供给函数为Q=20+6P。 (1)该商品的市场均衡价格和销售量是多少? (2)如果政府对该商品征收每单位商品4元的数量税,市场均衡的销售量是多少?消费者支付的价格和生产商接受的价格分别是多少?税收负担如何分配? (3)如果商品供给函数变为Q= 40+6P,题目(1)和(2)中的答案该如何变化?答案:解析:(1)联立需求函数和供给函数可得:100-2P=20+6P解得:均衡价格P=10。将P=10代入需求函数或供给函数可得销售量为80。 (2)如果政府对该商品征收每单位商品4元的数量税,均衡条件应满足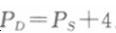
联立以下四个方程: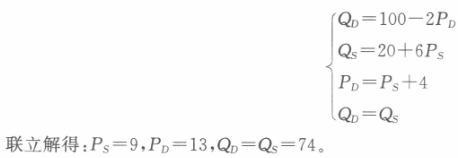
即市场均衡的销售量为74,消费者支付的价格为每单位13元,生产商接受的价格为每单位9元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 (3)联立需求函数和供给函数可得:100-2P=40+6P解得:均衡价格P=7.5。将P=7.5代入需求函数或供给函数可得销售量为85。如果政府对该商品征收每单位商品4元的数量税,均衡条件应满足PD—PS+4。联立以下四个方程: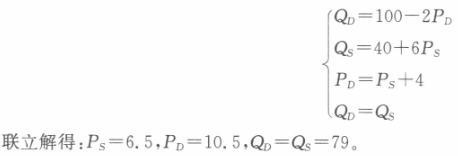
即市场均衡的销售量为79,消费者支付的价格为每单位10.5元,生产商接受的价格为每单位6.5元。每单位商品4元的税,其中消费者承担3元,生产者承担1元。 可以看出,由于供给曲线斜率不变,所以税负的转嫁程度不变,因为税负的转嫁程度取决于需求曲线和供给曲线的斜率。 -
第3题:
已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2=30元,该消费者的效用函数为U=3X1X,该消费者每年购买这两种商品的数量各应是多少?每年从中获得总效用是多少?
解二:根据预算线方程可以得出x 1 和x 2 的关系,即x 1 =27-1.5x 2 ,将其代入效用函数可以得出U=81x 2 2 -4. 5x 2 3 ,则求最大效用,即为求该效用函数的最大值,令其导数为零,可以得出x 2 =12,再代入关系式可得出x 1 =9,最后代入效用函数可得总效用为3888。 -
第4题:
假设在一个2×2的交换经济中消费者A和B交换两种商品z和y,消费者A的效用函数 是UA (XA,yA)=
,消费者B的效用函数是ub(xb,yB)=
他们拥有两种商品的初始 禀赋分别是WA(40,60)和WB(40,40)。标准化商品x的价格Px=1,商品y的价格为P。 (1)计算消费者A和B对两种商品z和y的需求函数。 (2)计算该交换经济的均衡价格及均衡配置。答案:解析:(1)消费者A、B各自的收入为40+60P、40+40P。 由柯布一道格拉斯效用函数的性质可知A的需求函数为:
B的需求函数为:
(2)联立消费者A、B关于商品z的需求函数可得: xA+xB =40+50P=80 解得:P=4/5 可得:xA =44,yA =55,XB =36,yB=45。 -
第5题:
某条无差异曲线是水平直线,这表明消费者对()的消费为中性(设X由横轴度量, Y由纵轴度量)。
A.商品Y
B.商品X
C.商品X和商品Y
D.商品X或商品Y
A
