itgle.com
设Ω是由：x2+y2+z2≤2z及z≤x2+y2所确定的立体区域，则Ω的体积等于：
题目
设Ω是由：x2+y2+z2≤2z及z≤x2+y2所确定的立体区域，则Ω的体积等于：
相似考题
更多“设Ω是由：x2+y2+z2≤2z及z≤x2+y2所确定的立体区域，则Ω的体积等于： ”相关问题
-
第1题：
Ω是由曲面z=x2+y2，y=x，y=0，z=1在第一卦限所围成的闭区域，f（x，y，z） 在Ω上连续，则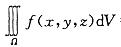
等于：
答案：C解析：提示：作出Ω的立体图形，并确定Ω在xOy平面上投影区域：Dxy：x2+y2 = 1，写出在直角坐标系下先z后x最后y的三次积分。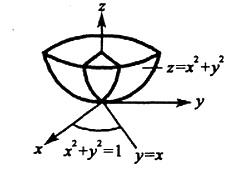
-
第2题：
若D是由x=0，y=0，x2+y2=1所围成在第一象限的区域，则二重积分
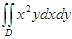
等于（ ）。
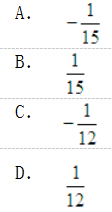答案：B解析：采用极坐标法求二重积分，具体计算如下：
-
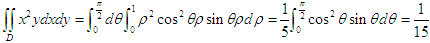
第3题：
曲面x2+ y2 + z2 = 2z之内以及曲面z = X2 +y2之外所围成的立体的体积V等于：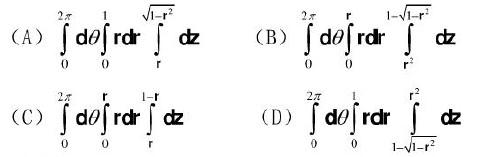
答案：D解析：解：选D.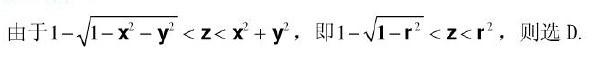
-
第4题：
设D为2≤x2+y2≤2x所确定的区域，则二重积分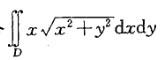
化为极坐标系下的二次积分时等于：
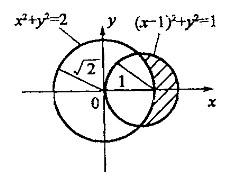
答案：D解析：提示:画出积分区域D的图形，由x2+y2≥2得知在圆x2+y2=2的外部，由x2+y2≤2x 得知在圆(x-1)2+y2=1的内部，D为它们的公共部分，如图画斜线部分。求交点，解方程组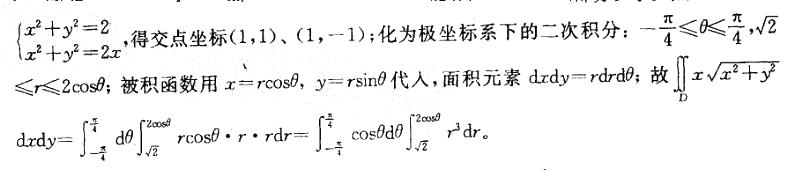
-
第5题：
设函数z=z(x，y)由方程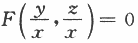
确定，其中F为可微函数，且F'2≠0，则
=A.Ax
B.z
C.-x
D.-z答案：B解析：
-
第6题：
计算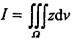
,其中Ω为z2=x2+y2，z=1所围成的立体，则正确的解法是( )。
答案：B解析：提示：在柱坐标下计算
-
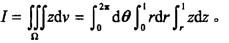
第7题：
若序列x（n）的Z变换为X（z），则（－0.5）nx（n）的Z变换为（）
- A、2X（2z）
- B、2X（-2z）
- C、X（2z）
- D、X（-2z）
正确答案:D -
第8题：
填空题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。正确答案： -1/7解析：
由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。 -
第9题：
单选题设z=f（x2+y2），其中f具有二阶导数，则等于（）．A2f’（x2+y2）
B4x2f（x2+y2）
C2’（x2+y2）+4x2f（x2+y2）
D2xf（x2+y2）
正确答案： D解析： 暂无解析 -
第10题：
单选题设方程x2＋y2＋z2＝4z确定可微函数z＝z（x，y），则全微分dz等于（ ）。[2014年真题]A（ydx＋xdy）/（2－z）
B（xdx＋ydy）/（2－z）
C（dx＋dy）/（2＋z）
D（dx－dy）/（2－z）
正确答案： C解析：
对等式两边分别同时求导，得：2xdx＋2ydy＋2zdz＝4dz。所以dz＝（xdx＋ydy）/（2－z） -
第11题：
单选题设z＝yφ（x/y），其中φ（u）具有二阶连续导数，则∂2z/（∂x∂y）等于（ ）。[2017年真题]A（1/y）φ″（x/y）
B（－x/y2）φ″（x/y）
C1
Dφ′（x/y）－（x/y）φ″（x/y）
正确答案： B解析：
计算得
∂z/∂x＝y·φ′（x/y）·（1/y）＝φ′（x/y）
∂2z/∂x∂y＝－（x/y2）φ″（x/y） -
第12题：
填空题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。正确答案： 1解析：
构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2 ，得fx′＝exyz2＋exy·2z·zx′，代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。 -
第13题：
曲面：x2+y2+z2=2z之内及曲面z=x2+y2之外所围成的立体的体积V等于：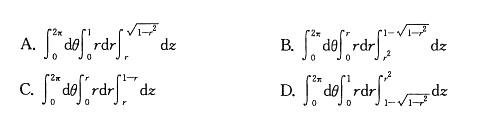
答案：D解析：
-
第14题：
设空间区域V：x2+y2+z2≤R2，则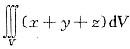
=( )。A、0
B、1
C、2
D、3答案：A解析：由于V关于三个坐标面都对称，而被积函数关于一个变量为奇函数，因此积分为零 -
第15题：
曲面x2+y2+z2=2z之内以及曲面z=x2+y2之外所围成的立体的体积V等于:
答案：D解析：提示:利用柱面坐标计算三重积分，立体体积
dV = rdrdθdz，写成三次积分即可。 -
第16题：
设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．答案：解析：
-
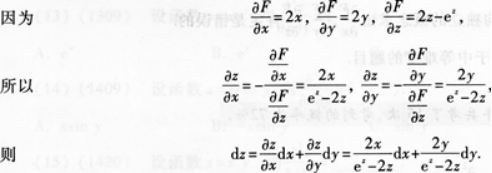
第17题：
设Ω是由平面x+y+z=1与三个坐标平面所围成的空间区域，则
=_________.答案：解析：
-
第18题：
（）是椭球面。
- A、Z=（X2+Y2）/-30
- B、X2/100+Y2/50+Z2/40=1
- C、Z=X2/30
- D、Z=X2/100-Y3/70
- E、X2+Y2+Z2=100
正确答案:B -
第19题：
设z=f（x2+y2），其中f具有二阶导数，则等于（）．
- A、2f’（x2+y2）
- B、4x2f"（x2+y2）
- C、2’（x2+y2）+4x2f"（x2+y2）
- D、2xf"（x2+y2）
正确答案:C -
第20题：
填空题设z＝f（x，xy）二阶偏导数连续，则∂2z/∂x∂y＝____。正确答案： f2′+xf12″+xyf22″解析：
∂z/∂x＝f1′＋yf2′，∂2z/（∂x∂y）＝f11″·0＋xf12″＋f2′＋yf22″·x＝xf12″＋f2′＋xyf22″ -
第21题：
填空题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋∂z/∂y＝____。正确答案： 2解析：
方程两边同时对x求偏导，则∂z/∂x＝e2x－3z（2－3∂z/∂x），可得∂z/∂x＝2e2x－3z/（1＋3e2x－3z）。同理∂z/∂y＝e2x－3z（－3∂z/∂y）＋2，可得∂z/∂y＝2/（1＋3e2x－3z），所以3∂z/∂x＋∂z/∂y＝6e2x－3z/（1＋3e2x－3z）＋2/（1＋3e2x－3z）＝2（1＋3e2x－3z）/（1＋3e2x－3z）＝2。 -
第22题：
单选题设z＝z（x，y）是由方程xz－xy＋ln（xyz）＝0所确定的可微函数，则∂z/∂y等于（ ）。[2013年真题]A－xz/（xz＋1）
B－x＋1/2
Cz（－xz＋y）/[x（xz＋1）]
Dz（xy－1）/[y（xz＋1）]
正确答案： B解析：
将xz－xy＋ln（xyz）＝0两边对y求偏导，得xzy′－x＋x（z＋y·zy′）/（xyz）＝0，整理得zy′＝z（xy－1）/[y（xz＋1）]。 -
第23题：
单选题设f有二阶偏导数，z＝f（xy），则∂2z/∂x∂y等于（ ）。Ayf″＋f′
Bxy2f″
Cxyf′f″
Df′＋xyf″
正确答案： B解析：
∂z/∂x＝yf′，∂2z/∂x∂y＝f′＋yf″·x＝f′＋xyf″。