设f(x)=2^x-1,则当x→0时,f(x)是x的()。A、高阶无穷小B、低阶无穷小C、等价无穷小D、同阶但不等价无穷
题目
设f(x)=2^x-1,则当x→0时,f(x)是x的()。
A、高阶无穷小
B、低阶无穷小
C、等价无穷小
D、同阶但不等价无穷
相似考题
更多“设f(x)=2^x-1,则当x→0时,f(x)是x的()。 ”相关问题
-
第1题:
设f(x)是周期为4的可导奇函数,且f'(x)=2(x-1),x∈[0,2],则f(7)=________.答案:1、1.解析:由f'(x)=2(x-1),x∈[0,2]知,f(x)=(x-1)^2+C.又f(x)为奇函数,则f(0)=0,C=-1.f(x)=(x-1)^2-1.由于f(x)以4为周期,则f(7)=f[8+(-1)]=f(-1)=-f(1)=1. -
第2题:
递归函数f(x,y)定义如下: f(x,y)=f(x-1,y)+f(x,y-1) 当x>0且y>0 f(x,y)=x+y 否则 则f(2,1)的值是()。
A.1
B.2
C.3
D.4
4 -
第3题:
【单选题】设f(x)=x(x-1)(x-2)……(x-99)(x-100),则f '(0)等于
A.-100;
B.0;
C.100;
D.100!
(1)由题意可得, f 1 (x)=(x+1)? e x , f 2 (x)=(x+2)? e x , f 3 (x)=(x+3)? e x ,…, 猜测出f n (x)的表达式 f n (x)=(x+n)? e x (n∈N*) . (2)由(1)可知, f n (x)=(x+n)? e x (n∈N*) , ∴ f ′ n (x)=(x+n+1)? e x , 令f′ n (x)=0,解得x=-(n+1), ∵当x>-(n+1)时,f' n (x)>0,当x<-(n+1)时,f' n (x)<0, ∴当x=-(n+1)时,f n (x)取得极小值 f n (-(n+1))=- e -(n+1) , 即f n (x)的极小值为 y n =- e -(n+1) (n∈N*) . (3)∵ g n (x)=- x 2 -2(n+1)x-8n+8 , ∴当x=-(n+1)时,g n (x)取最大值,即 a= g n (-(n+1))=(n-3 ) 2 , 又∵ b= f n (-(n+1))=- e -(n+1) , ∴a-b=(n-3) 2 +e -(n+1) , 问题转化为求 c n =(n-3 ) 2 + e -(n+1) 的最小值. 解法1(构造函数): 令h(x)=(x-3) 2 +e -(x+1) (x≥0), 则h'(x)=2(x-3)-e -(x+1) ,又h(x)在区间[0,+∞)上单调递增, ∴h'(x)≥h'(0)=-6-e -1 , 又∵h'(3)=-e -4 <0,h'(4)=2-e -5 >0, ∴存在x 0 ∈(3,4)使得h'(x 0 )=0, 又h'(x)在区间[0,+∞)上单调递增, ∴0≤x<x 0 时,h'(x 0 )<0,当x>x 0 时,h'(x 0 )>0, 即h(x)在区间[x 0 ,+∞)上单调递增,在区间[0,x 0 )上单调递减, ∴(h(x)) min =h(x 0 ). 又∵h(3)=e -4 ,h(4)=1+e -5 ,则h(4)>h(3), ∴当n=3时,a-b取得最小值e -4′ . 解法2(利用数列的单调性): ∵ c n+1 - c n =2n-5+ 1 e n+2 - 1 e n+1 , ∴当n≥3时,2n-5≥1, 1 e n+2 >0 , 1 e n+1 <1 , ∴ 2n-5+ 1 e n+2 - 1 e n+1 >0 , ∴c n+1 >c n . ∵ c 1 =4+ 1 e 2 , c 2 =1+ 1 e 3 , c 3 = 1 e 4 ,c 1 >c 2 >c 3 , ∴当n=3时,a-b取得最小值e -4 . -
第4题:
设f(x)函数在[0,+∞)上连续,且满足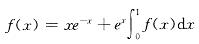 ,则f(x)是:
A. xe-x
,则f(x)是:
A. xe-x
B. xe-x-ex-1
C. ex-2
D. (x-1)e-x答案:B解析: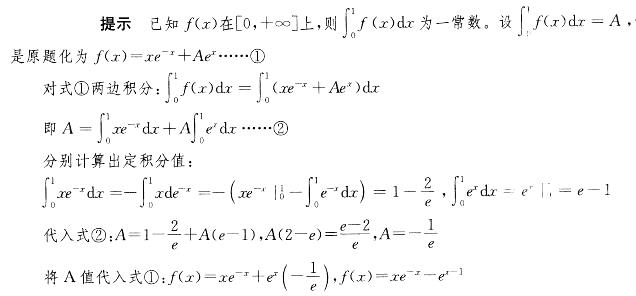
-
第5题:
设f(x)是(-∞,∞)是的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7.5)等于______。
A.0.5
B.-0.5
C.1.5
D.-1.5
A 试题分析: f ( x )是周期为2的奇函数,f(x)=f(x+2),当0≤ x ≤1时, f ( x )=2 x (1- x ),那么可知 f (- )=- f ( )=-f(2+ )=-f( )=-2 故答案为A. 点评:主要是考查了抽象函数的奇偶性和解析式的运用,属于基础题。
