itgle.com

写出符合下列条件的数： （1）最小的正整数 ； （2）最大的负整数； （3）大于-3且小于2的所有整数； （4）绝对值最小的有理数； （5）绝对值大于2且小于5的所有负整数； （6）在数轴上，与表示-1的点距离为2的所有数。

题目

写出符合下列条件的数：

   （1）最小的正整数 ；                                          （2）最大的负整数；

   （3）大于-3且小于2的所有整数；                        （4）绝对值最小的有理数；

   （5）绝对值大于2且小于5的所有负整数；

   （6）在数轴上，与表示-1的点距离为2的所有数。

相似考题

1.分别列出一个满足下列条件的整数：（1） 所有的加数是负整数，和是-5； （2）一个加数是0，和是-5；（3）至少有一个加数是正整数，和是-5。

2.绝对值大于1小于5的所有整数的和是多少？

3.除以7余5，除以5余2，除以3余l的所有三位数中的最小正整数是（ ）。A．292B．397C．502D．187

4.下列说法是否正确？请将错误的改正过来。（1）所以的有理数都能用数轴上的点表示 ； （2）符号不同的两个数互为相反数；（3）有理数分为正数和负数； （4）两数相加，和一定大于任何一个数；（5）两数相减，差一定小于被减数。

更多“写出符合下列条件的数：（1）最小的正整数 ；（2）最大的负整数；（3）大于-3且小于2的所有整数；（4）绝对值最小的有理数；（5）绝对值大于2且小于5的所有负整数；（6）在数轴上，与表示-1的点距离为2的所有数。”相关问题

  • 第1题：

    假设用12个二进制位表示数据。它能表示的最大无符号整数为(1)；若采用原码，它能表示的最小负整数为(2)。

    A．2047

    B．2048

    C．4095

    D．4096


    正确答案：C

  • 第2题：

    绝对值大于或等于1，而小于4的所有的正整数的和是（ ）

    A 8 B 7 C 6 D 5


    正确答案：C

  • 第3题：

    数学理解

    填空题：

         （1）一个数的平方等于它本身，这个数是________;

         （2）平方根等于本身的数是________;

         （3）算术平方根等于本身的数是________;

         （4）立方根等于本身的数是___________;

         （5）大于0且小于π的整数是________;

         （6）满足                 的整数x是_____________;


    （1）0.1

    （2）0

    （3）0.1

    （4）0.1，-1

    （5）1,2,3

    （6）-1,0,1,2

  • 第4题：

    判断下列说法是否正确：

    （1）无限小数都是无理数；

    （2）无理数都是无限小数；

    （3）带根号的数都是无理数；

    （4）所有有理数都可以用数轴上的点表示，反过来，数轴上的所有点都表示有理数；

    （5）所有实数都可以用数轴上的点表示，反过来，数轴上的所有点都表示实数。


    （1）错误

    （2）正确

    （3）错误

    （4）错误

    （5）正确


  • 第5题：

    设M和N为正整数,且M>2,N>2,MN<2(M＋N),满足上述条件的例(M,N)共有()对。A.3B.5C.6D.7

    设M和N为正整数，且M>2，N>2，MN<2（M+N），满足上述条件的例(M,N)共有（）对。

    A.3

    B.5

    C.6

    D.7


    正确答案：B

  • 第6题：

    SNMPv2中规定Gauge32最大值是(59)。

    A．232

    B．232-1

    C．小于232的任意正整数

    D．任意正整数


    正确答案：C
    解析：简单网络管理协议SNMPv2管理信息结构定义中，Gauge32是一个具有“可增可减、保持最大”特性的计量器，其最大值可以是小于232的任意正整数。

  • 第7题：

    设M和N为正整数，且 M>2 ，N>2，MN<2（M+N），满足上述条件的例(M,N)共有（ ）对。

    A.3
    B.5
    C.6
    D.7

    答案：B
    解析：

  • 第8题：

    满足∣a-b∣+ab=1的非负整数对（a,b）的个数是

    A.1
    B.2
    C.3
    D.4
    E.5

    答案：C
    解析：

  • 第9题：

    SNMPv2中规定Gauge32最大值是（）。

    • A、2^32-1
    • B、2^32
    • C、小于2^32的任意正整数
    • D、任意正整数

    正确答案:A

  • 第10题：

    根据现代观点，数轴上的数是（）

    • A、实数
    • B、自然数
    • C、正整数
    • D、有理数

    正确答案:A

  • 第11题：

    单选题
    正整数d是序列α=a0，a1，a2…的一个周期，满足ai+d=ai，i=0，1，2…成立的最小正整数d称为α的什么？（）
    A

    最大正周期

    B

    基础周期

    C

    周期和

    D

    最小正周期


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    SNMPv2中规定Gauge32最大值是（）。
    A

    2^32-1

    B

    2^32

    C

    小于2^32的任意正整数

    D

    任意正整数


    正确答案： B
    解析： 暂无解析

  • 第13题：

    下列说法正确的是（ ）

    A 整数就是正整数和负整数 B 负整数的相反数就是非负整数

    C 有理数中不是负数就是正数 D 零是自然数，但不是正整数


    正确答案：D

  • 第14题：

    画一条数轴，并在数轴上表示：3.5和它的相反数，－4和它的倒数，绝对值等于3的数，最大的负整数和它的平方，并把这些数由小到大用“<”号连接起来。


    正确答案：
    解:数轴略;

    -3.5-3-2-1-0.5133.5

  • 第15题：

    根据下列条件求正整数x：

    （1）x+2＜6 ；（2）2x+5＜10；

    （3）x-3/2≥2x-5/3；（4）2+x/2≥2x-1/3-2.


    (1) x+26               （2）2x+510

    x4                    x2.5

    则x可取1, 2, 3               则x可取1， 2

    （3）x-3 /22x-5/3      （4）2+x/22x-1/3-2

    两边同时乘以6得：             两边同时乘以6得：

    3（x-3）2（2x-5）            3（2+x） 2(2x-1)-12

    3x-9 4x-10    x≤1                 x ≤ 20

    则x可取1                                                             则x可取1,2，…, 20.


  • 第16题：

    （1）有没有最小的正整数？有没有最小的整数？

    （2）有没有最小的有理数？有没有最小的无理数？

    （3）有没有最小的正实数？有没有最小的实数？


    解：（1）有最小的正整数1，没有最小的整数；

    （2）没有最小的有理数，没有最小的无理数；

    （3）没有最小的正实数，没有最小的实数。


  • 第17题：

    用数0、1、2、3、4能够组成多少个小于1000的没有重复数字的正整数?

    A．4

    B．16

    C．48

    D．68


    正确答案：D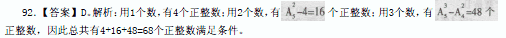

  • 第18题：

    用数0、1、2、3、4能够组成多少个小于1000的没有重复数字的正整数?

    A． 4

    B．16

    C．48

    D．68


    正确答案：D
    用1个数，有4个正整数；用2个数，有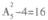个正整数；用3个数，有个正整数，因此总共有4+16+8=68个正整数满足条件。

  • 第19题：

    有理数是正整数、负整数、正分数、负分数和零的统称，此有理数概念的定义方法是（　　）．

    A.递归定义
    B.关系定义
    C.外延定义
    D.发生关系

    答案：C
    解析：
    外延定义即概念的外延，整数和分数统称为有理数，正整数、负整数和零统称为整数，正分数和负分数统称为分数.

  • 第20题：

    正整数d是序列α=a0，a1，a2…的一个周期，满足ai+d=ai，i=0，1，2…成立的最小正整数d称为α的什么？（）

    • A、最大正周期
    • B、基础周期
    • C、周期和
    • D、最小正周期

    正确答案:D

  • 第21题：

    每一个确定的正整数a，都有一个确定的后继数a’，a’也是正整数（一个数的后继数就是紧接在这个数后面的数，例如，1的后继数是2，2的后继数是3等等）.那么1（）任何正整数的后继数。


    正确答案:不是

  • 第22题：

    令A为正整数集合，定义A上的关系R：a R b当且仅当2a≤b+1，下列有序对属于R的是（）。

    • A、（2，2）
    • B、（3，2）
    • C、（6，15）
    • D、（15，6）

    正确答案:C

  • 第23题：

    单选题
    将一个正整数n表示成一系列正整数之和，n=n1+n2+…+nk（其中，n1≥n2≥…≥nk≥1，k≥1）正整数n的一个这种表示称为正整数n的一个划分。正整数n的不同的划分个数总和称为正整数n的划分数，记作p（n）；另外，在正整数n的所有不同划分中，将最大加数n1不大于m的划分个数记作q（n，m）。则当n=10时，p（n）=（）。
    A

    q（8，8）

    B

    1+q（9，9）

    C

    2+q（10，8）

    D

    ABC都正确


    正确答案： A
    解析： 暂无解析

相关内容