itgle.com

设离散型随机变量x的分布函数为则Y=X^2+1的分布函数为_______.

题目
设离散型随机变量x的分布函数为

则Y=X^2+1的分布函数为_______.

相似考题

1.设随机变量X~B（1，0.8）（二项分布），则X的分布函数为___________.

2.设离散型随机变量X的分布列为则P(1A．0.5B．0.3C．0.4D．0.15

3.设离散型随机变量X的分布列如表5.1-2所示，则E(X)为( )。A．1B．2.7C．2.8D．3

4.设随机变量X~B(1,0.8),则X的分布函数为()。

更多“设离散型随机变量x的分布函数为 ”相关问题

  • 第1题：

    设随机变量x的分布函数为



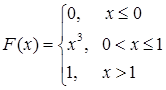
    则数学期望E（X）等于（　　）。



    答案：B
    解析：

  • 第2题：

    设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().



    A.F(z)=F（-x）
    B.F(x)=F（-x）
    C.F(X)=F（-x）
    D.f(x)=f（-x）

    答案：C
    解析：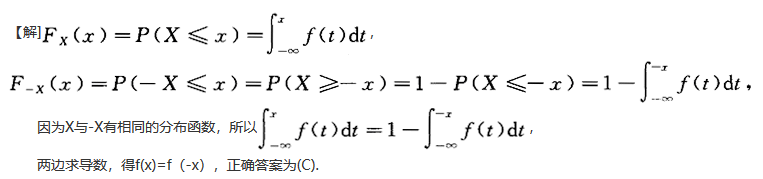

  • 第3题：

    设随机变量X,Y相互独立,它们的分布函数为Fx(x),F(y),则Z=min{X,Y}的分布函数为().


    答案：C
    解析：
    FZ(z)=P(Z≤z)=P(min{X,Y}≤z)=1-P(min{X,Y}>z)　　=1-P(X>z,Y>z)=1-P(X>z)P(Y>z)
    　　=1-【1-P(X≤z)】【1-P(Y≤z)】=1-【1-FX(z)】【1-FY(z)】，选(C).

  • 第4题：

    设随机变量X的分布函数为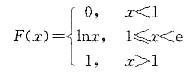 则X的概率密度函数f(x)为( )。


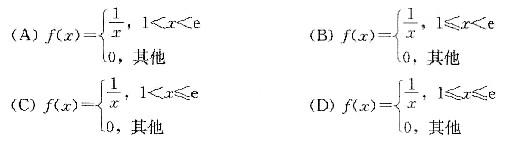    答案：B
    解析：
    由分布函数与概率密度函数关系f(x)=F'(x)，当1≤x＜e时，f(x)=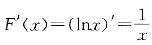，X的概率密度综合表示为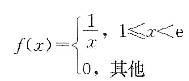

  • 第5题：

    设离散型随机变量x的分布列为

    ①求常数a的值；
    ②求X的数学期望E(X)．


    答案：
    解析：
    ①随机变量的分布列必须满足规范性，所以0．2+a+0．5=1，得a=0．3．②E(X)=1×0．2+2×0．3+3×0．5=2．3．

  • 第6题：

    设连续型随机变量X的分布函数为F(x)=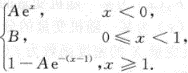
    　　(1)求常数A,B;(2)求X的密度函数f(x)；(3)求P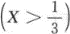


    答案：
    解析：

  • 第7题：

    设二维离散型随机变量(X，Y)的概率分布为
    　　
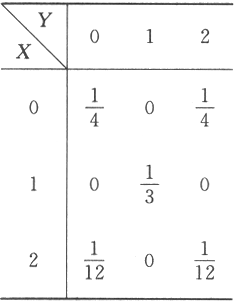
    　　(Ⅰ)求P{X=2Y)；
    　　(Ⅱ)求Cov(X-Y，Y).


    答案：
    解析：

  • 第8题：

    设随机变量X的分布函数为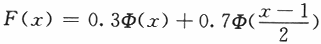，其中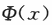为标准正态分布的分布函数，则E(X)=

    A.A0
    B.0.3
    C.0.7
    D.1

    答案：C
    解析：

  • 第9题：

    设随机变量X的分布函数为求随机变量X的概率密度和概率


    答案：
    解析：
    解：本题考查概率密度概念的简单应用。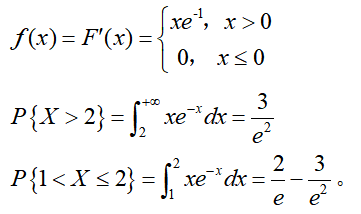

  • 第10题：

    问答题
    9.设离散型随机变量X的分布律为 求x的分布函数，以及概率P{1.50.5}．

    正确答案：
    解析：

  • 第11题：

    问答题
    33.设随机变量X的分布函数为

    正确答案：
    解析：

  • 第12题：

    多选题
    对随机变量的分布列、密度函数与分布函数，下列表述中正确的有（　　）。[2008年真题]
    A

    用分布列和密度函数描述离散随机变量的分布

    B

    用分布列和分布函数描述离散随机变量的分布

    C

    用分布列和分布函数描述连续随机变量的分布

    D

    用密度函数和分布函数描述连续随机变量的分布

    E

    用密度函数和分布函数描述离散随机变量的分布


    正确答案： B,C
    解析：
    离散随机变量的分布可用分布列表示。作为一个分布，满足以下两个条件：pi≥0，p1+p2+…+pn=1，满足这两个条件的分布称为离散分布，这一组pi又称为分布的概率函数。即用分布列和分布函数来描述离散随机变量分布。连续随机变量X的分布可用概率密度函数p（x）表示，连续随机变量X的分布函数F（x）可用其密度函数算得。反之，概率密度函数p（x）也可从分布函数F（x）求出。即用密度函数和分布函数来描述连续随机变量的分布。

  • 第13题：

    设随机变量X的分布函数


    答案：C
    解析：

  • 第14题：

    设随机变量X的密度函数为f(x),且f(x)为偶函数,X的分布函数为F(x),则对任意实数a,有().



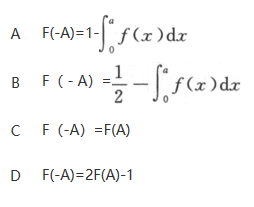    答案：B
    解析：

  • 第15题：

    设随机变量X,Y的分布函数分别为F1(x),F2(x),为使得F(x)=aF1(x)＋bF2(x)为某一随机变量的分布函数,则有().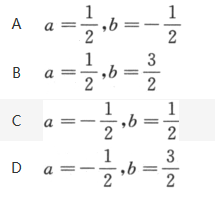


    答案：D
    解析：
    根据性质F(+∞)=1，得正确答案为(D).

  • 第16题：

    设离散型随机变量X的概率分布为

    求X的数学期望EX及方差DX．


    答案：
    解析：

  • 第17题：

    设二维随机变量(X,Y)的联合密度函数为f(x,y)=
    　　(1)求随机变量X,Y的边缘密度函数；
    　　(2)判断随机变量X,Y是否相互独立；
    　　(3)求随机变量Z=X+2Y的分布函数和密度函数.


    答案：
    解析：

  • 第18题：

    设随机变量X和Y相互独立,且分布函数为Fx(x)=,Fy(y)=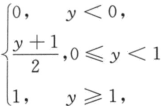,令U=X+Y,则U的分布函数为_______.


    答案：
    解析：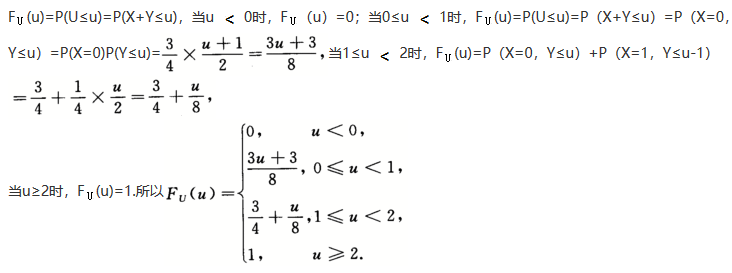

  • 第19题：

    设随机变量X的概率密度为令随机变量，
    　　(Ⅰ)求Y的分布函数；
    　　(Ⅱ)求概率P{X≤Y}.


    答案：
    解析：
    【分析】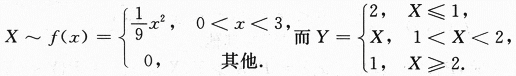
    Y是随机变量X的函数，只是这函数是分段表示的，这样得到的Y可能是非连续型，也非离散型，
    【解】(Ⅰ)设Y的分布函数为FYy)，显然P{1≤Y≤2}=1，所以，
    当y<1时，FY(y)=P{Y≤y)=0；
    当1≤y<2时，FY(y)=P{Y≤y}=P{Y<1}+P{Y=1}+P{1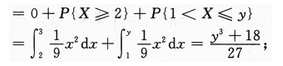
    当2≤y时，FY(y)=P{Y≤y}=P{Y≤2}=1.
    总之，Y的分布函数为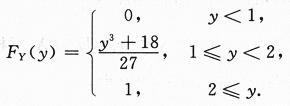

    (Ⅱ)因为Y=

  • 第20题：

    设随机变量X的分布函数为，其中为标准正态分布函数，则EX=________.


    答案：1、2.
    解析：

  • 第21题：

    设离散型随机变量X的分布列如表5 -2所示，则E（X）为（ ）。


    A. 1.0 B. 2.7 C. 2.8 D. 3.0


    答案：C
    解析：

  • 第22题：

    问答题
    4.设离散型随机变量x的分布律为

    正确答案：
    解析：

  • 第23题：

    填空题
    设离散型随机变量X服从于参数为λ（λ＞0）的泊松分布，已知P{X＝1}＝P{X＝2}，则λ＝____。

    正确答案： 2
    解析：
    根据题意λe－λ/1!＝λ2e－λ/2!，得λ＝2。

相关内容