itgle.com

设F1(x)与F2(x)为两个分布函数，其相应的概率密度f1(x)与f2(x)是连续函数，则必为概率密度的是A.Af1(x)f2(x) B.2f2(x)F1(x) C.f1(x)F2(x) D.f1(x)F2(x)+f2(x)f1(x)

题目
设F1(x)与F2(x)为两个分布函数，其相应的概率密度f1(x)与f2(x)是连续函数，则必为概率密度的是



A.Af1(x)f2(x)
B.2f2(x)F1(x)
C.f1(x)F2(x)
D.f1(x)F2(x)+f2(x)f1(x)
相似考题

1.设R、N分别表示实数、整数和自然数集,下面定义函数f1、f2、f3:f1:R→R,f(x)=2xf2:N→N×N,f(n)=f设R、N分别表示实数、整数和自然数集，下面定义函数f1、f2、f3： f1：R→R，f(x)=2x f2：N→N×N，f(n)=＜n，n+1＞ f3：N→N，f(x)=x mod 3，x除以3的余数 则下面说法正确的是( )。A．f1和f2是单射但不是满射函数B．f1和f3都是满射函数C．f2是双射函数D．以上说法全都是错误的

2.已知（X,Y）服从均匀分布，联合概率密度函数为设Z=max｛X,Y｝求Z的概率密度函数fz(z)

3.已知函数fl()、f2()的定义如下图所示设调用函数f1时传递给形参x的值是1，若函数调用f2(a)采用引用调用(call by refere nce)的方式传递信息，则函数n的返回值为 (32) ；若函数调用f2(a)以值调用(call liy value)的方式传递信息，则函数F1返回值为(33)。A.-5B.6C.15D.35

4.设X的概率密度与分布函数分别为f(x)和F(X),则下列选项正确是 ( )A.P{X=x}=f(x)B.P{X=x}=F(x)C.P{X=x}D.0

更多“设F1(x)与F2(x)为两个分布函数，其相应的概率密度f1(x)与f2(x)是连续函数，则必为概率密度的是 ”相关问题

  • 第1题：

    设F1(x)与F2(x)分别为随机变量X1与X2的分布函数。为使F(x)=aF1(x)-bF2(x)成为某一随机变量的分布函数，则a与b分别是：


    答案：A
    解析：

  • 第2题：

    设随机变量X的分布函数为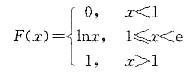 则X的概率密度函数f(x)为( )。


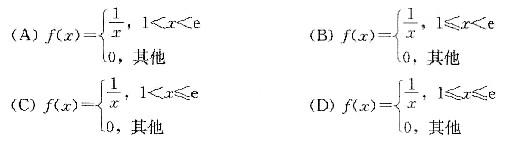    答案：B
    解析：
    由分布函数与概率密度函数关系f(x)=F'(x)，当1≤x＜e时，f(x)=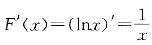，X的概率密度综合表示为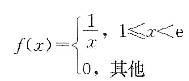

  • 第3题：

    设随机变量X的概率密度函数为fxcx)=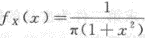,则y=2X的密度函数为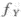(y)=_______.


    答案：
    解析：
    因为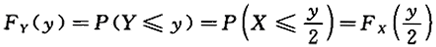，　　所以.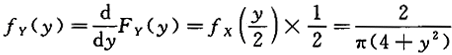

  • 第4题：

    设f1(x)为标准正态分布的概率密度，f2(x)为［-1，3］上均匀分布的概率密度，若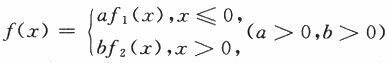为概率密度，则a，b应满足

    A.A2a+3b=4
    B.3a+2b=4
    C.a+b=1
    D.a+b=2

    答案：A
    解析：

  • 第5题：

    设随机变量X的分布函数为求随机变量X的概率密度和概率


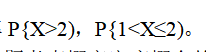    答案：
    解析：
    解：本题考查概率密度概念的简单应用。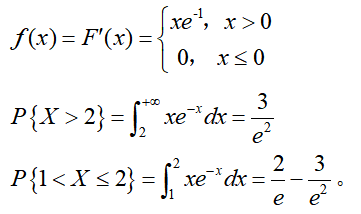

  • 第6题：

    设F1（x）与F2（x）分别为随机变量X1与X2的分布函数。为使F（x）=aF1（x）-bF2（x）成为某一随机变量的分布函数，则a与b分别是：（）

    • A、a=3／5，b=-2／5
    • B、a=2／3，b=2／3
    • C、a=-1／2，b=3／2
    • D、a=1／2，b=-2／3

    正确答案:A

  • 第7题：

    设X1，X2是任意两个相互独立的连续型随机变量，它们的概率密度分别为f1（x）与f2（x），分布函数分别为F1（x）与F2（x），则（）

    • A、f1（x）+f2（x）必为某一随机变量的概率密度
    • B、f1（x）f2（x）必为某一随机变量的概率密度
    • C、F1（x）+F2（x）必为某一随机变量的分布函数
    • D、F1（x）F2（x）必为某一随机变量的分布函数

    正确答案:D

  • 第8题：

    设随机变量X的概率密度为fX（x），随机变量Y的概率密度为fY（y），则二维随机变量（X、Y）的联合概率密度为fX（x）fY（y）。


    正确答案:错误

  • 第9题：

    问答题
    39.设X的概率密度为 求：(1)X的分布函数F(x)；    (2)P{X一0.5}．

    正确答案：
    解析：

  • 第10题：

    单选题
    设f1（x），f2（x）是二阶线性齐次方程y″＋p（x）y′＋q（x）y＝0的两个特解，则c1f1（x）＋c2f2（x）（c1，c2是任意常数）是该方程的通解的充要条件为（　　）。
    A

    f1（x）f2′（x）－f2（x）f1′（x）＝0

    B

    f1（x）f2′（x）＋f1′（x）f2（x）＝0

    C

    f1（x）f2′（x）－f1′（x）f2（x）≠0

    D

    f1′（x）f2（x）＋f2（x）f1（x）≠0


    正确答案： A
    解析：
    要使c1f1（x）＋c2f2（x）是方程y″＋p（x）y′＋q（x）y＝0的通解，则须满足f1（x），f2（x）线性无关，即ψ（x）＝f1（x）/f2（x）≠k（k为常数）。则ψ′（x）＝[f1′（x）f2（x）－f1（x）f2′（x）]/f22（x）≠0，即f1′（x）f2（x）－f1（x）f2′（x）≠0。

  • 第11题：

    单选题
    设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程（　　）的解。
    A

    y′＋P（x）y＝f1（x）＋f2（x）

    B

    y＋P（x）y′＝f1（x）－f2（x）

    C

    y＋P（x）y′＝f1（x）＋f2（x）

    D

    y′＋P（x）y＝f1（x）－f2（x）


    正确答案： A
    解析：
    根据题意可知，y1′＋P（x）y1＝f1（x），y2′＋P（x）y2＝f2（x）。两式相加得（y1′＋y2′）＋P（x）（y1＋y2）＝f1（x）＋f2（x）。则可发现y＝y1＋y2是方程y′＋P（x）y＝f1（x）＋f2（x）的解。

  • 第12题：

    单选题
    设X～N（2，22），其概率密度函数为f（x），分布函数F（x），则（　　）。
    A

    P{X≤0}＝P{X≥0}＝0.5

    B

    f（－x）＝1－f（x）

    C

    F（x）＝－F（－x）

    D

    P{X≥2}＝P{X＜2}＝0.5


    正确答案： B
    解析：
    该正态分布的密度函数的图像关于x＝μ＝2对称，故P{X≥2}＝P{X＜2}＝0.5，故应选D。

  • 第13题：

    设随机变量X,Y的分布函数分别为F1(x),F2(x),为使得F(x)=aF1(x)＋bF2(x)为某一随机变量的分布函数,则有().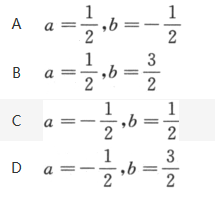


    答案：D
    解析：
    根据性质F(+∞)=1，得正确答案为(D).

  • 第14题：

    已知函数f132、f232的定义如下图所示。设调用函数f1时传递给形参x的值是1，若函数调用f2(a)采用引用调用(call by reference)的方式传递信息，则函数f1的返回值为(请作答此空)；若函数调用f2(a)以值调用(call by value)的方式传递信息，则函数f1的返回值为( )。

    A.-5
    B.6
    C.15
    D.35

    答案：C
    解析：
    本题考查程序语言基础知识。
    函数f1被调用而运行时，其局部变量值的变化情况如下：在调用f2(a)之前，x的值为1，a的值为5。在以引用调用方式调用f2(a)时，形参x是实参a的引用，在函数f2中的x就是函数f1中a的别名(或者说此时x与a所对应的存储单元是同一个，只是角度不同而已)，因此执行函数f2时，条件表达式x＞1即等同于a＞1，a的值是5所以该条件表达式成立，从而执行了"x=x*x"，就将x所对应存储单元的内容改为了25，然后结束f2的执行并将所返回的-10赋值给f1中的x，因此在f1结束时返回的值为a+x=25-10=15。
    在值调用方式下调用f2(a)时，是将实参a的值5传递给f2的形参x，a和x所对应的存储单元是不同的，此后执行f2时，由于x的值是5，所以条件表达式x＞1即等同于5＞1，是成立的，从而执行了"x=x*x"，此时是将f2中的x修改为25，与f1中的a和x都无关，在结束f2的执行并将返回值-10赋值给f1中的x后，f1结束时进行的计算为a+x=5-10=-5。

  • 第15题：

    设随机变量X与Y独立，其中X的概率分布为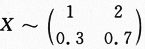而Y的概率密度为f(y)，求随机变量U=X+Y的概率密度g(u).


    答案：
    解析：
    【简解】本题是2003年数三的考题，考查一个离散型和一个连续型两个随机变量的函数的分布，随机变量的独立性等，
    先求分布函数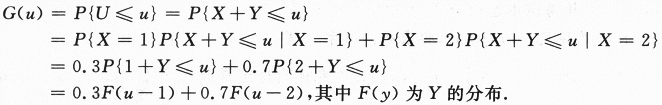

    由此得g(u)=0.3f(u-1)+0.7f(u-2).

  • 第16题：

    设随机变量x的概率密度为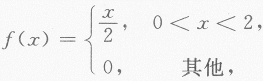F(x)为X的分布函数，EX为X的数学期望，则P{F(X)>EX-1}=________.


    答案：
    解析：

  • 第17题：

    已知 X1 和 X2 是相互独立的随机变量，分布函数分别为F1（x）和F2（x），则下列选项一定是某一随机变量分布函数的为（ ）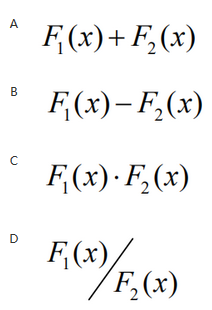


    答案：C
    解析：
    分布函数要满足非负性，规范性，单调不减性，右连续性.

  • 第18题：

    设F1（x）与F2（x）为两个分布函数，其相应的概率密度f1（x）与f2（x）是连续函数，则必为概率密度的是（）

    • A、f1（x）f2（x）
    • B、2f2（x）F1（x）
    • C、f1（x）F2（x）
    • D、f1（x）F2（x）+f2（x）F1（x）

    正确答案:D

  • 第19题：

    设f1（x）和f2（x）为二阶常系数线性齐次微分方程y″+py′+g=0的两个特解，若由f1（x）和f2（x）能构成该方程的通解，下列哪个方程是其充分条件（）？

    • A、f1（x）·f′2（x）-f2（x）f′1（x）=0
    • B、f1（x）·f′2（x）-f2（x）·f′1（x）≠0
    • C、f1（x）f′2（x）+f2（x）·f′1（x）=0
    • D、f1（x）f′2（x）+f2（x）f′1（x）≠0

    正确答案:B

  • 第20题：

    单选题
    有以下程序：#include main(){　int x[]={8,2,6,12,5,15},f1,f2;　int *p=x;　f1=f2=x[0];　for(;p　{　　if(f1　　if(f2>*p)f2=*p;　}　printf("%d,%d",f1,f2);}程序的运行结果是（　　）。
    A

    15,2

    B

    15,15

    C

    2,15

    D

    8,8


    正确答案： A
    解析：
    本题求数组的最大值和最小值，首先把数组x首地址的值赋给指针p，故*p初始值为8，而p是地址值，p+1相当于数组中下一元素的地址，在for循环，是求数组x对应的最大值和最小值，f1为最大值，f2为最小值。因此输出为15和2。答案选择A选项。

  • 第21题：

    单选题
    设f1（x）和f2（x）为二阶常系数线性齐次微分方程y″+py′+q=0的两个特解，若由f1（x）和f2（x）能构成该方程的通解，下列哪个方程是其充分条件？（）
    A

    f1（x）f′2（x）-f2（x）f′1（x）=0

    B

    f1（x）f′2（x）-f2（x）f′1（x）≠0

    C

    f1（x）f′2（x）+f2（x）f′1（x）=0

    D

    f1（x）f′2（x）+f2（x）f′1（x）≠0


    正确答案： C
    解析： 暂无解析

  • 第22题：

    单选题
    设F1（x）与F2（x）分别为随机变量X1与X2的分布函数。为使F（x）=aF1（x）-bF2（x）成为某一随机变量的分布函数，则a与b分别是：（）
    A

    a=3／5，b=-2／5

    B

    a=2／3，b=2／3

    C

    a=-1／2，b=3／2

    D

    a=1／2，b=-2／3


    正确答案： C
    解析： 暂无解析

  • 第23题：

    问答题
    10.设F1(x)，F2(x)分别为随机变量X1和X2的分布函数，且F(x)=aF1(x)一bF2(x)也是某一随机变量的分布函数，证明a—b=1．

    正确答案：
    解析：

相关内容