已知（X,Y）服从均匀分布，联合概率密度函数为设Z=max｛X,Y｝求Z的概率密度函数fz(z)

第1题：

设二维随机变量(X，Y)在区域上服从均匀分布，令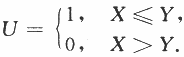
　　(Ⅰ)写出(X，Y)的概率密度；
　　(Ⅱ)请问U与X是否相互独立？并说明理由；
　　(Ⅲ)求Z=U+X的分布函数F(z).

答案：

解析：

第2题：

设随机变量（X,Y)服从均匀分布U（D), 其中D={（x,y): 0＜x＜y＜1}, 则T=X+Y的概率密度函数为p（t)=max（1-|1-t|,0).

第3题：

设正态随机变量X和Y相互独立， X-N（mu=1,sigma=2), Y-N（mu=1,sigma=2), 试求Z=X+Y的概率密度函数

第4题：

设随机变量X,Y相互独立，且X的概率分布为P{X=0)=P{X=2)=，Y的概率密度为
　　(Ⅰ)求P{Y≤EY}；
　　(Ⅱ)求Z=X+Y的概率密度.

答案：

解析：

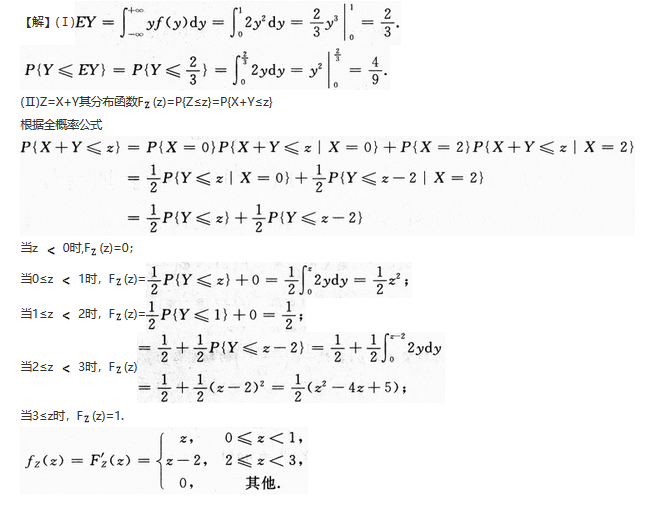
第5题：

设随机变量（X, Y）在区域D={（x,y):0＜x＜1,|y|＜x}上服从均匀分布，求随机变量X的边缘概率密度函数。