设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。

题目

相似考题

1.设随机变量X和Y都服从标准正态分布,则()。A、X+Y服从正态分布B、X2+Y2服从χ2分布C、X2和Y2都服从χ2分布D、X2/Y2服从正态分布

2.设随机变量X服从正态分布N（2，4），Y服从均匀分布U（3，5），则E（2X-3Y）= __________.

3.若随机变量X服从正态分布N(a,b),随机变量Y服从正态分布N(c,d),则X＋Y所服从的分布为正态分布。()此题为判断题(对，错)。

4.设随机变量和是相互独立的随机变量且都服从正态分布,X~N(3,4),Y~N(2,9),求D(3X＋4Y)=()

参考答案和解析

答案：

解析：

解：本题考查一些重要分布的数字特征与参数之间的关系。E（X）=1，E（y）=2 E（2X-y+3）=2E（X）-E（y）+3=3。

更多“设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。”相关问题

第1题：

设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。
A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布
B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布
C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布
D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布

正确答案：D
解析：中心极限定理指出，无论共同的分布是什么，只要随机变量的个数n相当大时，的分布总近似于正态分布。
第2题：

设随机变量X服从正态分布N(μ，16)，Y服从正态分布N(μ，25).记p=P(X≤μ-4)，q=P(Y≥μ+5)，则p与q的大小关系是( ).

A.p＞q
B.p＜q
C.p=q
D.不能确定

答案：C
解析：
第3题：

设随机变量X,Y相互独立且都服从标准正态分布,令U=X^2+Y^2.求：
　　(1）(u);(2)P{U>D(U)｜U>E(U)}.

答案：
解析：
第4题：

设二维随机变量(X，Y)服从正态分布N(μ，μ；σ^2，σ^2；0)，则E(XY^2)=________.

答案：
解析：
第5题：

设随机变量X与Y相互独立，X的概率分布为P{X=1}=P{X=-1}=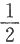，Y服从参数为λ的泊松分布.令Z=XY.
　　(Ⅰ)求Cov(X，Z);
　　(Ⅱ)求Z的概率分布.

答案：
解析：
第6题：

设随机变量X服从参数λ=2的泊松分布，则P（X≥1）=（）

正确答案:1-e^-2
第7题：

设随机变量X服从正态分布N（μ₁，σ²₁），随机变量Y服从正态分布N（μ₂，σ²₂），且P{|X-μ₁|<1}>P{|Y-μ₂|<1}，则必有（）
- A、σ₁<σ₂
- B、σ₁>σ₂
- C、μ₁<μ₂
- D、μ₁>μ₂
正确答案:A
第8题：

设随机变量X服从参数为2的泊松分布，则E（2X）=（）

正确答案:4
第9题：

设随机变量X服从泊松分布，E（X）=6，证明：P{3

正确答案:1/3
第10题：

设随机变量X服从参数为2的泊松分布，且Y=3X-2，求E（Y）。

正确答案:由于X服从参数为2的泊松分布，
因此EX=2，
故E（Y）=E（3X-2）=3EX-2=4
第11题：

单选题
设随机变量X服从正态分布N（-1，9），则随机变量Y=2-X服从（）．
A
正态分布N（3，9）
B
均匀分布
C
正态分布N（1，9）
D
指数分布

正确答案： D
解析：按定理1，Y是X的线性函数，y依然服从正态分布，由k=-1、c=2算得y服从正态分布 N（2-(-1)，（-1)2×9)=N(3,9). 故选(A).
第12题：

单选题
设随机变量X服从正态分布N（μ，16），Y服从正态分布N（μ，25）.记p=P（X≤μ-4），g=P（Y≥μ+5），则p与q的大小关系是（）．
A
p>q
B
p
C
p=q
D
不能确定

正确答案： B
解析：暂无解析
第13题：

设随机变量X和Y都服从标准正态分布，则

A.X+Y服从正态分布.
B.X^2+Y^2服从χ^2分布.
C.X^2和Y^2都服从χ^2分布.
D.X^2/Y^2服从F分布，

答案：C
解析：
(方法一)X和Y均服从N(0，1).故X^2和Y^2都服从χ^2(1)分布.答案应选(C).(方法二)(A)不成立，因题中条件既没有X与Y相互独立，也没有假定(X，Y)正态，故就保证不了X+Y正态.(B)和(D)均不成立，因为没有X与Y的相互独立，所以也没有X^2与Y^2相互独立，答案应选(C).【评注】我们可以小结正态分布一维和二维间的关系如下：(1)当(X，Y)正态时，X与Y均正态，且任何aX+bY也正态，反之，X与Y均正态，不能保证(X，Y)二维正态，也不能保证aX+bY正态.如果对任何aX+bY均正态，则(X，Y)二维正态.(2)当X与Y均正态且相互独立是指(X，Y)二维正态，且相关系数ρXY=0
第14题：

设随机变量X服从参数为2的泊松分布,令Y=4X-3,则E(Y)=_______,D(Y)=_______.

答案：1、32
解析：
因为X～P(2)，所以E(X)=D(X)=2，于是E(Y)=4E(X)-3=5，D(Y)=16D(X)=32.
第15题：

设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求：
　　(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).

答案：
解析：
第16题：

设随机变量X的概率分布为P{X=1}=P{X=2}=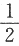，在给定X=i的条件下，随机变量Y服从均匀分布U(0，i)(i=1，2).
　　(Ⅰ)求Y的分布函数FY(y)；
　　(Ⅱ)求EY.

答案：
解析：
第17题：

已知随机变量X服从正态分布N(μ，σ2)，设随机变量Y=2X，那么Y服从的分布是()。

A.N(2μ，2σ2)

B.N(4μ，4σ2)

C.N(2μ，4σ2)

D.N(μ，σ2)

答案：C
解析：
由于随机变量X服从正态分布N(μ，σ2)，则随机变量Y=2X的均值为2μ，方差为4σ2，即Y服从的分布是N(2μ，4σ2)。
第18题：

设随机变量X₁，X₂，X₃相互独立，其中X₁在[0，6]上服从均匀分布，X₂服从正态分布N（0，2²），X₃服从参数为λ=3的泊松分布，记Y=X₁-2X₂+3X₃。则DY=（）。

正确答案:46
第19题：

设随机变量X服从参数为2的泊松分布，且Y=3X-2，则E（Y）=（）。

正确答案:4
第20题：

设X服从0—1分布，P=0.6，Y服从λ=2的泊松分布，且X，Y独立，则X+Y（）.
- A、服从泊松分布
- B、仍是离散型随机变量
- C、为二维随机向量
- D、取值为0的概率为0
正确答案:B
第21题：

设随机变量X服从正态分布N（-1，9），则随机变量Y=2-X服从（）．
- A、正态分布N（3，9）
- B、均匀分布
- C、正态分布N（1，9）
- D、指数分布
正确答案:A
第22题：

设随机变量X服从正态分布N（μ，16），Y服从正态分布N（μ，25）.记p=P（X≤μ-4），g=P（Y≥μ+5），则p与q的大小关系是（）．
- A、p>q
- B、p
- C、p=q
- D、不能确定
正确答案:C
第23题：

单选题
设随机变量X服从正态分布N（μ1，σ12），Y服从正态分布N（μ2，σ22），且P{|X－μ1|＜1}＞P{|Y－μ2|＜1}，则必有（　　）。
A
σ₁＜σ₂
B
σ₁＞σ₂
C
μ₁＜μ₂
D
μ₁＞μ₂

正确答案： A
解析：
根据题意，有：P{|（X－μ₁）/σ₁|＜1/σ₁}＞P{|（Y－μ₂）/σ₂|＜1/σ₂}，故1/σ₁＞1/σ₂⇒σ₁＜σ₂。

itgle.com

设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。

题目

相似考题

参考答案和解析

更多“设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。”相关问题

相关内容