itgle.com

一个口袋内有4个不同的红球，6个不同的白球. (1)从中任取4个球，红球的个数不比白球少的取法有多少种? (2)若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种?

题目
一个口袋内有4个不同的红球，6个不同的白球.
(1)从中任取4个球，红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种?

相似考题

1.口袋里有3个红球和2个白球，球除颜色外完全相同，从中任意摸出1个球。那么，摸出红球的可能性是_____，摸出白球的可能性是_____。要使它们的可能性相同，可以怎么做？

2.在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球？A．14 B．15 C．17 D．18

3.：新年晚会上，老师让每位同学从一个装有许多玻璃球的口袋中取两个球，这些球的手感相同。只有红、黄、白、蓝、绿五色之分，结果发现总有两个人取的球相同，由此可知，参加取球的至少有（ ）人。A．15B．16C．17D．18

4.一个布袋里有大小相同而颜色不同的木球，其中红球10个，白球9个，蓝球2个，黄球8个。一次至少取多少个球，才能保证其中4个是同色球?()A.4B.10C.13D.12

参考答案和解析
答案：
解析：
解：(1)由题意知本题是一个分类计数问题.将取出4个球分成三类情况：取4个红

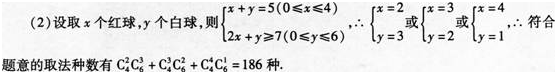
更多“一个口袋内有4个不同的红球，6个不同的白球. ”相关问题

  • 第1题：

    从装有2个红球和2个白球的袋内任取2球,那么互不相容的两个事件是________。

    A．“至少一个白球”与“都是白球”

    B．“至少一个白球”与“至少一个红球”

    C．“恰有一个白球”与“恰有两个白球”

    D．“至多一个白球”与“都是红球”


    正确答案：C
    解析：设“取到红球为1”,“取到白球为0”,则样本空间共有四个样本点,Ω={(0,0),(0,1),(1,0),(1,1)};“至少一个白球”={(0,0),(0,1),(1,0)};“都是白球”={(0,0)};“至多一个白球”=“至少一个红球”={(1,1),(0,1),(1,0)};“都是红球”={(1,1)};“恰有一个白球”={(0,1),(1,0)};“恰有两个白球”={(0,0)),所以答案A、B是相容事件,D是对立事件.C才是互不相容的事件。

  • 第2题：

    （3）一个口袋内装有除颜色外其他都相同的6个白球和4个红球，从中任意摸出2个，求：A、2个都是白球的概率；B、2个都是红球的概率；C、一个白球，一个红球的概率。


    正确答案：
              

  • 第3题：

    一个口袋内有4个不同的红球，6个不同的白球，若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种?

    A．3

    B．120

    C．180

    D．186


    正确答案：D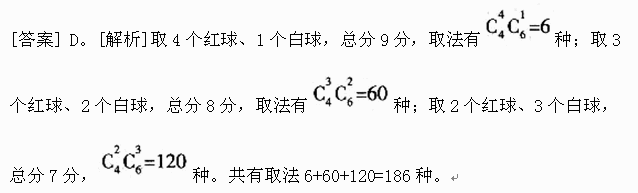

  • 第4题：

    设口袋中有10只红球和15只白球,每次取一个球,取后不放回,则第二次取得红球的概率为_______.


    答案：
    解析：
    设A1={第一次取红球)，A2={第一次取白球），B={第二次取红球），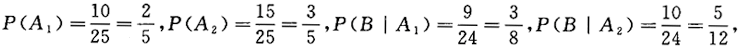　　

    则
    　　

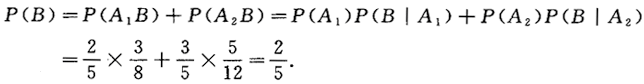
  • 第5题：

    从5个不同的黑球和2个不同的白球中,任选3个球放入3个不同的盒子中,每盒1球,其中至多有1个白球的不同放法共有（ ）种

    A.160
    B.165
    C.172
    D.180
    E.182

    答案：D
    解析：

  • 第6题：

    一口袋中有3个红球和2个白球，某人从该口袋中随机摸出一球，摸得红球得5分，摸得白球得2分，则他所得分数的数学期望为（ ）

    A.2.5；
    B.3.5；
    C.3.8；
    D.以上都不对

    答案：C
    解析：

  • 第7题：

    口袋中放有3只红球和11只黄球，这两种球除颜色外没有任何区别，随机从口袋中任取一只球，取到黄球的概率是______．


    答案：
    解析：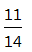

  • 第8题：

    一个盒子内装有大小、形状相同的四个球，其中红球1个、绿球1个、白球2个，小明摸出一个球不放回，再摸出一个球，则两次都摸到白球的概率是__________。


    答案：
    解析：

  • 第9题：

    口袋里装有10只外形相同的球，其中7只红球，3只白球．从口袋中任意取出2只球，则它们是一只红球、一只白球的概率等于（）．

    • A、21/90.
    • B、21/45
    • C、21/100
    • D、21/50

    正确答案:B

  • 第10题：

    袋内有红球1个、白球7个，随意从袋中摸出一球，摸到红球事件的信息量为（）比特。

    • A、1
    • B、7/8
    • C、1/8
    • D、3

    正确答案:D

  • 第11题：

    单选题
    在一个口袋里有黑球、白球、红球、蓝球各13个，则至少取出几个球才能保证有6个相同颜色的球（）
    A

    24

    B

    23

    C

    22

    D

    21


    正确答案： D
    解析： 根据最差原则，先取出黑球、白球、红球、蓝球各5个，最后任意取出1个球，都能保证有6个颜色相同的球。5×4+1=21。

  • 第12题：

    单选题
    口袋里装有10只外形相同的球，其中7只红球，3只白球．从口袋中任意取出2只球，则它们是一只红球、一只白球的概率等于（）．
    A

    21/90.

    B

    21/45

    C

    21/100

    D

    21/50


    正确答案： C
    解析： 暂无解析

  • 第13题：

    有关C语言的问题

    口袋中有红、黄、蓝、白、黑五种颜色的球若干，每次从口袋中取出3个球。问得到三种不同颜色球的可能选取方法，打印出三种颜色的各种组合。


    循环遍历即可。if (i != j && j !=k && k!=i) -- 三种不同颜色的条件#include <stdio.h>#include <stdlib.h>void main(){int i,j,k,n=0;char c[5][7]={"red","yellow","blue","white","black"};for (i=0;i<5;i++)for (j=i+1;j<5;j++)for (k=j+1;k<5;k++){ if (i != j && j !=k && k!=i) printf("%s %s %s\n",c[i],c[j],c[k]); n++;};printf("n=%d",n);}得：red yellow bluered yellow whitered yellow blackred blue whitered blue blackred white blackyellow blue whiteyellow blue blackyellow white blackblue white blackn=10

  • 第14题：

    在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球?

    A．14

    B．15

    C．17

    D．18


    正确答案：B
    [答案] B。解析：抽屉原理，最坏的情况是10个黑球和4个红球都拿出来了，第15次拿到的肯定是白球。

  • 第15题：

    现有三个箱子,第一个箱子有4个红球,3个白球；第二个箱子有3个红球,3个白球；第三个箱子有3个红球,5个白球；先取一只箱子,再从中取一只球,(1)求取到白球的概率；(2)若取到红球,求红球是从第二个箱子中取出的概率.


    答案：
    解析：

  • 第16题：

    袋中有12只球,其中红球4个,白球8个,从中一次抽取两个球,求下列事件发生的概率：
    　　(1)两个球中一个是红球一个是白球；
    　　(2)两个球颜色相同.


    答案：
    解析：
    【解】(1)令A={抽取的两个球中一个是红球一个是白球}，则.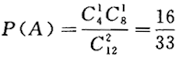
    (2)令B={抽取的两个球颜色相同}，则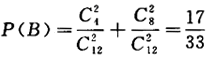

  • 第17题：

    甲盒内有红球4只,黑球2只,白球2只;乙盒内有红球5只,黑球3只;丙盒内有黑球2只,白球2只,从这三只盒子的任意一只中任取出一只球,它是红球的概率是（ ）

    A.0.5625
    B.0.5
    C.0.45
    D.O.375
    E.0.225

    答案：D
    解析：

  • 第18题：

    一个口袋中有4个白球，1个红球，7个黄球．搅匀后随机从袋中摸出1个是白球的概率是_________．


    答案：
    解析：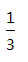

  • 第19题：

    一个口袋中有7个红球3个白球,从袋中任取一球,看过颜色后是白球则放回袋中，直至取到红球,然后再取一球，假设每次取球时各个球被取到的可能性相同，求第一、第二次都取到红球的概率（ ）。

    A.7/10
    B.7/15
    C.7/20
    D.7/30

    答案：B
    解析：
    设AB分别表演一、二次取红球，则有P（AB）=P（A）P（B|A）=7/106/9=7/15。

  • 第20题：

    已知一个口袋里有5个红球，6个白球，7个黑球，则至少取出多少个球才能保证有一个红球和一个白球？（）

    • A、3个
    • B、9个
    • C、13个
    • D、14个

    正确答案:D

  • 第21题：

    一口袋有6个白球，4个红球，“无放回”地从袋中取出3个球，则事件“恰有两个红球”的概率为（）


    正确答案:3/10

  • 第22题：

    问答题
    8.袋中有7个球，其中红球5个白球2个，从袋中取球两次，每次随机地取一个球，取后不放回，求：    (1)第一次取到白球、第二次取到红球的概率；    (2)两次取得一红球一白球的概率．

    正确答案：
    解析： 暂无解析

  • 第23题：

    单选题
    已知一个口袋里有5个红球，6个白球，7个黑球，则至少取出多少个球才能保证有一个红球和一个白球？（）
    A

    3个

    B

    9个

    C

    13个

    D

    14个


    正确答案： D
    解析： 暂无解析

相关内容