设向量α=(1,2,-2),β=(2,a,3),且α与β正交,则a=_________.
题目
设向量α=(1,2,-2),β=(2,a,3),且α与β正交,则a=_________.
相似考题
更多“设向量α=(1,2,-2),β=(2,a,3),且α与β正交,则a=_________. ”相关问题
-
第1题:
设α1,α2,…,αn为n个线性无关的n维列向量,且与向量β正交.证明:向量β为零向量.答案:解析:
-
第2题:
若两个向量(3,-1,1),(1,2,t)正交,则 t =().
A.0
B.1
C.-1
D.2
A -
第3题:
设 a=(2,−1,2)a=(2,−1,2),向量 xx与aa 平行,且 a⋅x=−18a⋅x=−18, 则 x=
A.(−4,2,−4)
B.(4,−2,4)
C.±(4,−2,4)
D.有无穷多解
由题设条件,有0=|3E+A|=|(-1)(-3E-A)|=(-1) 4 |3E-A|=|-3E-A|,故A有一个特征值为λ=-3. 由AA T =2E两端取行列式,得|A| 2 =16,又|A|<0,故|A|=-4. 因|A|≠0,故A可逆,于是由特征值与特征向量的性质3,可知A * 有一个特征值为4/3.设A为可逆矩阵,若λ为A的一个特征值,则1/ ? ? λ ? ? 为A*的一个特征值;若μ为A*的一个特征值,则1/μ为A的一个特征值.一般地有:λ[ 1 ,λ 2 ,…,λ n 为可逆矩阵A的全部特征值 1/为A * 的全部特征值. -
第4题:
设α1=(1,2,-1,0)^T,α2=(1,1,0,2)^T,α3=(2,1,1,α)^T.若由α1,α2,α3生成的向量空间的维数为2,则α=________.答案:1、6.解析:本题考查向量空间及其维数的概念,因为α1,α2,α3所生成的向量空间是2维,亦即向量组的秩r(α1,α2,α3)=2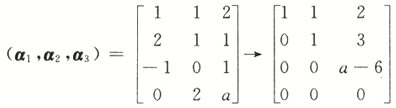
由秩为2,知α=6. -
第5题:
设向量组线性无关,则总可以找到一组正交向量,使得正交向量组与线性无关向量组等价。
线性无关
