itgle.com

线性回归模型中误差的含义是（ ）。A.回归直线的截距 B.除X和Y线性关系之外的随机因素对Y的影响 C.回归直线的斜率 D.观测值和估计值之间的残差

题目
线性回归模型中误差的含义是（ ）。

A.回归直线的截距
B.除X和Y线性关系之外的随机因素对Y的影响
C.回归直线的斜率
D.观测值和估计值之间的残差
相似考题

1.DW检验中要求有假定条件，在下列条件中不正确的是（）A.解释变量为非随机的B.随机误差项为一阶自回归形式C.线性回归模型中不应含有滞后内生变量为解释变量D.线性回归模型只能为一元回归形式

2.描述两个变量之间相关关系的最简单的回归模型是()。A.非线性回归模型 B.一元线性回归模型 C.多元线性回归模型 D.经验回归模型

3.线性回归模型Y=β+β1X+ε中误差项目ε的含义是()。A.回归直线的截距 B.除X和Y线性关系之外的随机因素对Y的影响 C.回归直线的斜率 D.观测值和估计值之间的残差

4.一元线性回归模型中，随机误差项ε需满足（ ）。

更多“线性回归模型中误差的含义是（ ）。”相关问题

  • 第1题：

    下列回归模型中，属于一元线性回归模型的是（ ）。



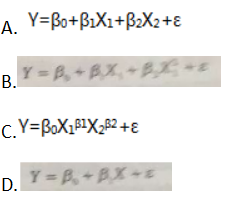    答案：D
    解析：
    回归模型可以用描述因变量Y如何依赖自变量X和误差项ε的方程来表示。只涉及一个自变量的一元线性回归模型可以表示为： Y = β0 + β1 X + ε
    式中β0 和 β1为模型的参数
    y 是 x 的线性函数（β0 + β1 X）加上误差项ε。

  • 第2题：

    非线性回归模型，按其形式和估计方法的不同，可以分为（ ）。
    ?Ⅰ.非标准线性回归模型
    ?Ⅱ.可线性化的非线性回归模型
    ?Ⅲ.不可线性化的非线性回归模型
    ?Ⅳ.非回归模型

    A.Ⅰ、Ⅱ
    B.Ⅱ、Ⅲ
    C.Ⅰ、Ⅱ、Ⅲ
    D.Ⅰ、Ⅲ、Ⅳ

    答案：C
    解析：
    非线性回归模型，按其形式和估计方法的不同，可以分为非标准线性回归模型、可线性化的非线性回归模型、不可线性化的非线性回归模型。

  • 第3题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型中关于随机项μi的基本假设是（　　）。


    答案：A,B,C,D
    解析：

  • 第4题：

    线性回归模型y=β0+β1x+u中，随机误差产生的原因有（）

    • A、模型设定误差
    • B、对y的观测误差
    • C、对β0的估计错误
    • D、对β1的估计错误
    • E、各种细小的偶然误差

    正确答案:B,E

  • 第5题：

    线性回归模型中误差项的含义是（）

    • A、回归直线的截距
    • B、回归直线的斜率
    • C、观测值和估计值之间的残值
    • D、除X和Y线性关系之外的随机因素对Y的影响

    正确答案:D

  • 第6题：

    DW检验中要求有假定条件，在下列条件中不正确的是（）

    • A、解释变量为非随机的
    • B、随机误差项为一阶自回归形式
    • C、线性回归模型中不应含有滞后内生变量为解释变量
    • D、线性回归模型只能为一元回归形式

    正确答案:D

  • 第7题：

    多重线性回归模型中偏回归系数的含义是什么？


    正确答案:偏回归系数的含义是：在控制其他自变量的水平不变的情况下，该自变量每改变一个单位，反应变量平均改变的单位数。

  • 第8题：

    单选题
    线性回归模型Y=β0+β1X+ε中误差项目的含义是(    )。
    A

    回归直线的截距

    B

    除X和Y线性关系之外的随机因素对Y的影晌

    C

    回归直线的斜率

    D

    观测值和估计值之间的残差


    正确答案： D
    解析：

  • 第9题：

    单选题
    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是（　　）。Ⅰ．被解释变量与解释变量之间具有线性关系Ⅱ．随机误差项服从正态分布Ⅲ．各个随机误差项的方差相同Ⅳ．各个随机误差项之间不相关
    A

    Ⅰ、Ⅱ、Ⅲ

    B

    Ⅰ、Ⅲ、Ⅳ

    C

    Ⅱ、Ⅲ、Ⅳ

    D

    Ⅰ、Ⅱ、Ⅲ、Ⅳ


    正确答案： A
    解析：
    一元线性回归模型为：yi＝α＋βxi＋ui（i＝1，2，3，…，n），其中yi为被解释变量；xi为解释变量；ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下：①每个ui均为独立同分布，服从正态分布的随机变量，且E（ui）＝0，V（ui）＝σ2＝常数；②随机项ui与自变量的任一观察值xi不相关，即Cov（ui，xi）＝0。

  • 第10题：

    单选题
    线性回归模型Y＝β0＋β1X＋ε中误差项ε的含义是（　　）。[2015年、2013年真题]
    A

    回归直线的截距

    B

    回归直线的斜率

    C

    观测值和估计值之间的残差

    D

    除x和y线性关系之外的随机因素对y的影响


    正确答案： C
    解析：
    线性回归模型y＝β0＋β1X＋ε中，β0＋β1X反映了由于自变量X的变化而引起的因变量Y的线性变化；误差项ε是个随机变量，表示除X和Y的线性关系之外的随机因素对Y的影响，是不能由X和Y的线性关系所解释的Y的变异性。

  • 第11题：

    单选题
    在多元线性回归模型中，若某个解释变量对其余解释变量的判定系数接近1，则表明 模型中存在（）
    A

    异方差

    B

    自相关

    C

    多重共线性

    D

    设定误差


    正确答案： C
    解析： 暂无解析

  • 第12题：

    问答题
    多重线性回归模型中偏回归系数的含义是什么？

    正确答案： 偏回归系数的含义是：在控制其他自变量的水平不变的情况下，该自变量每改变一个单位，反应变量平均改变的单位数。
    解析： 暂无解析

  • 第13题：

    回归分析是期货投资分析中重要的统计分析方法,而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）
    Ⅰ.被解释变量与解释变量之间具有线性关系
    Ⅱ.随机误差项服从正态分布
    Ⅲ.各个随机误差项的方差相同
    Ⅳ.各个随机误差项之间不相关

    A：Ⅰ.Ⅱ.Ⅲ.Ⅳ
    B：Ⅰ.Ⅲ.Ⅳ
    C：Ⅰ.Ⅱ.Ⅳ
    D：Ⅱ.Ⅲ.Ⅳ

    答案：A
    解析：
    —元线性回归模型为：yi=a+βi+mi（i=l,2,3,*,n）,其中yi为解解释变量Xi为解释变量;ui是一个随机变垦量.称为随机项。要求随机项u和自变量，Xi满足的统计假定如下：①每个ui均为独立同分右（IID、）,服从正态分右的随机变量，E（ui）=0,V（ui）=σ＾2常数②随机项ui与自变量的任一观察值Xi不相关，即COV（ui,i）=0

  • 第14题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）。
    I 被解释变量与解释变量之间具有线性关系
    Ⅱ 随机误差项服从正态分布
    Ⅲ 各个随机误差项的方差相同
    Ⅳ 各个随机误差项之间不相关

    A.I、Ⅱ、Ⅲ
    B.I、Ⅲ、Ⅳ
    C.Ⅱ、Ⅲ、Ⅳ
    D.I、Ⅱ、Ⅲ、Ⅳ

    答案：D
    解析：
    一元线性回归模型为：Yi=α+βxi+ui，(i=1，2，3，…，n)，其中Yi为被解释变量，xi为解释变量，ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下：①每个ui均为独立同分布，服从正态分布的随机变量，且E(ui)=0， V(ui)=σ2=常数；②随机项ui与自变量的任一观察值xi不相关，即Cov(ui，xi)=0．

  • 第15题：

    在线性回归模型中假设误差服从（）分布。


    正确答案:正态

  • 第16题：

    在多元线性回归模型中，若某个解释变量对其余解释变量的判定系数接近1，则表明 模型中存在（）

    • A、异方差
    • B、自相关
    • C、多重共线性
    • D、设定误差

    正确答案:A

  • 第17题：

    模型y=x1+2x2+3x3是属于（）

    • A、一元线性回归模型
    • B、多元线性回归模型
    • C、非线性回归模型
    • D、多元非线性回归模型

    正确答案:D

  • 第18题：

    如果线性回归模型中随机误差项的方差不是（），则称随机误差项具有异方差性。


    正确答案:常数

  • 第19题：

    在人力资源预测中，最常用的模型是（）

    • A、线性回归预测模型
    • B、时间序列预测模型
    • C、一元线性回归预测模型
    • D、多元线性回归模型

    正确答案:A

  • 第20题：

    单选题
    线性回归模型Y=β0+β1X+Ɛ中误差项Ɛ的含义是（  ）。
    A

    除X和Y线性关系之外的随机因素对y的影响

    B

    回归直线的截距

    C

    回归直线的斜率

    D

    观测值和估计值之间的残差


    正确答案： D
    解析：

  • 第21题：

    单选题
    在人力资源预测中，最常用的模型是（）
    A

    线性回归预测模型

    B

    时间序列预测模型

    C

    一元线性回归预测模型

    D

    多元线性回归模型


    正确答案： B
    解析： 暂无解析

  • 第22题：

    填空题
    在线性回归模型中假设误差服从（）分布。

    正确答案： 正态
    解析： 暂无解析

  • 第23题：

    单选题
    模型y=x1+2x2+3x3是属于（）
    A

    一元线性回归模型

    B

    多元线性回归模型

    C

    非线性回归模型

    D

    多元非线性回归模型


    正确答案： D
    解析： 暂无解析

相关内容