itgle.com

设矩阵A与B等价，则必有（ ） A.A的行向量与B的行向量等价 B.A的行向量与B的行向量等价 C.Ax=0与Bx=0同解 D.Ax=0与Bx=0的基础解系中向量个数相同

题目
设矩阵A与B等价，则必有（ ）

A.A的行向量与B的行向量等价
B.A的行向量与B的行向量等价
C.Ax=0与Bx=0同解
D.Ax=0与Bx=0的基础解系中向量个数相同
相似考题

1.设A是方阵,如有矩阵关系式AB=AC,则必有()A、A=0B、B≠C时A=0C、A≠0时B=CD、|A|≠0时B=C

2.设A和B均为n阶矩阵，则必有（ ）。A.｜A+B｜=｜A｜+｜B｜ B.AB=BA C.｜AB｜=｜BA｜ D.

3.设三阶矩阵，若A的伴随矩阵的秩等于1，则必有A.a=b或a+2b=0 B.a=b或a+2b≠0 C.a≠b且a+2b=0 D.a≠b且a+2b≠0

4.设矩阵A与B相似，则A与B的行列式值()

更多“设矩阵A与B等价，则必有（ ） ”相关问题

  • 第1题：

    设A为三阶可逆方阵，则( )与A等价。

    A.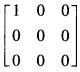
    B.
    C.
    D.

    答案：B
    解析：
    利用可逆阵与单位阵等价。

  • 第2题：

    设N阶矩阵A与对角矩阵合同,则A是().

    A.可逆矩阵
    B.实对称矩阵
    C.正定矩阵
    D.正交矩阵

    答案：B
    解析：

  • 第3题：

    设A是方阵，如有矩阵关系式AB=AC，则必有( ).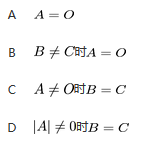


    答案：D
    解析：

  • 第4题：

    设A为n阶矩阵,且｜A｜=0,则A().

    A.必有一列元素全为零
    B.必有两行元素对应成比例
    C.必有一列是其余列向量的线性组合
    D.任一列都是其余列向量的线性组合

    答案：C
    解析：
    因为|A|=0，所以r(A)小于n，从而A的n个列向量线性相关，于是其列向量中至少有一个向量可由其余向量线性表示，选(C).

  • 第5题：

    设矩阵与等价，则a＝


    答案：
    解析：

  • 第6题：

    设A和B均为n阶矩阵，则必有（ ）。《》（ ）



    答案：C
    解析：

  • 第7题：

    设A和B均为n阶矩阵(n>1)，m是大于1的整数，则必有(　　)。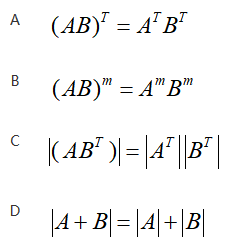


    答案：C
    解析：
    本题考查矩阵运算的相关性质。

  • 第8题：

    设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。

    • A、等价
    • B、相似
    • C、合同
    • D、正交

    正确答案:B

  • 第9题：

    单选题
    设n阶矩阵A与B等价，则必有（　　）。
    A

    当｜A｜＝a（a≠0）时，｜B｜＝a

    B

    当｜A｜＝a（a≠0）时，｜B｜＝－a

    C

    当｜A｜≠0时，｜B｜＝0

    D

    当｜A｜＝0时，｜B｜＝0


    正确答案： D
    解析：
    若矩阵A与B等价，则r（A）＝r（B），所以，若|A|＝0，则r（A）＜n，即r（B）＜n，有|B|＝0，同理知若|A|≠0，则|B|≠0。

  • 第10题：

    单选题
    设A是m×n矩阵，B是n×m矩阵，则（　　）。
    A

    当m＞n时，必有｜AB｜≠0

    B

    当m＞n时，必有｜AB｜＝0

    C

    当n＞m时，必有｜AB｜≠0

    D

    当n＞m时，必有｜AB｜＝0


    正确答案： C
    解析：
    因r（AB）≤min[r（A），r（B）]≤min（m，n），且AB为m×m矩阵，则当m＞n时，由r（AB）≤n，知AB为不可逆矩阵，故必有|AB|＝0。

  • 第11题：

    单选题
    设A是n阶矩阵，若|A|=0，则（　　）成立.
    A

    A的任一列向量是其余列向量的线性组合

    B

    必有一列向量是其余向量的线性组合

    C

    必有两列元素对应成比例

    D

    必有一列元素全为O


    正确答案： D
    解析：
    由|A|=0，知矩阵A的列向量线性相关，故至少有一列向量是其余列向量的线性组合．

  • 第12题：

    设A，B为n阶矩阵，考虑以下命题：①若A，B为等价矩阵，则A，B的行向量组等价②若行列式.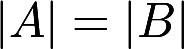，则A，B为等价矩阵③若与都只有零解，则A，B为等价矩阵④若A，B为相似矩阵，则与的解空间的维数相同以上命题中正确的是（ ）.

    A.①③
    B.②④
    C.②③
    D.③④

    答案：D
    解析：

  • 第13题：

    设矩阵A,B,C均为n阶矩阵，若AB=C，且B可逆，则（ ）


    A.矩阵C的行向量组与矩阵A的行向量组等价
    B.矩阵C的列向量组与矩阵A的列向量组等价
    C.矩阵C的行向量组与矩阵B的行向量组等价
    D.矩阵C的行向量组与矩阵B的列向量组等价


    答案：B
    解析：

  • 第14题：

    设A是实对称矩阵，C是实可逆矩阵，.则（ ）.

    A.A与B相似
    B.A与B不等价
    C.A与B有相同的特征值
    D.A与B合同

    答案：D
    解析：

  • 第15题：

    设n阶矩阵A与B等价, 则必须


    答案：D
    解析：

  • 第16题：

    设A，B，C均为n阶矩阵，若AB=C，且B可逆，则



    A.A矩阵C的行向量组与矩阵A的行向量组等价
    B.矩阵C的列向量组与矩阵A的列向量组等价
    C.矩阵C的行向量组与矩阵B的行向量组等价
    D.矩阵C的列向量组与矩阵B的列向量组等价

    答案：B
    解析：
    对矩阵A，C分别按列分块，记A=(α1，α2，…，αn)，C=(γ，γ，…，γ).　　由AB=C有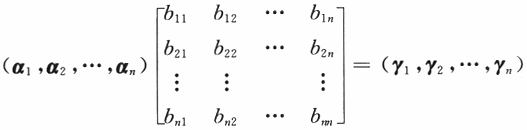

    　　可见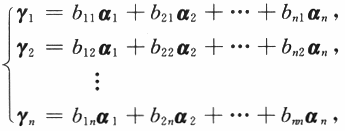

    即C的列向量组可以由A的列向量组线性表出.
    　　因为B可逆，有CB^-1=A.类似地，A的列向量组也可由C的列向量组线性表出，因此选(B).

  • 第17题：

    设A是m×n矩阵，如果m

    A.Ax=b必有无穷多解

    B.Ax=b必有唯一解

    C.Ax=0必有非零解

    D.Ax=0必有唯一解

    答案：C
    解析：
    根据条件可知，方程组中方程的个数一定小于未知数的个数，所以Ax=0必有非零解。由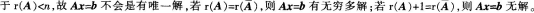

  • 第18题：

    设T=（t1，t2，„„，tn）为概率向量，P=（Pij）n*n为概率矩阵，则当k→∞时，必有（）

    • A、TPk等于P的平衡概率矩阵
    • B、TPk不等于P的平衡概率矩阵
    • C、TPk与P的平衡概率矩阵中的任一行向量都相等
    • D、TPk与P的平衡概率矩阵中的任一行向量都不相等

    正确答案:C

  • 第19题：

    设3阶方阵A有特征值2，且已知|A|=5，则A的伴随矩阵必有特征值（）．

    • A、25
    • B、12.5
    • C、5
    • D、2.5

    正确答案:D

  • 第20题：

    单选题
    设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。
    A

    等价

    B

    相似

    C

    合同

    D

    正交


    正确答案： B
    解析： 由相似矩阵的定义知B正确。故选B。

  • 第21题：

    单选题
    设3阶方阵A有特征值2，且已知|A|=5，则A的伴随矩阵必有特征值（）．
    A

    25

    B

    12.5

    C

    5

    D

    2.5


    正确答案： D
    解析： 暂无解析

  • 第22题：

    单选题
    设A是m×n矩阵，B是n×m矩阵，则（　　）.
    A

    当m＞n时，必有%7cAB%7c≠0

    B

    当m＞n时，必有%7cAB%7c=0

    C

    当n＞m时，必有%7cAB%7c≠0

    D

    当n＞m时，必有%7cAB%7c=0


    正确答案： D
    解析：
    因r（AB）≤min[r（A），r（B）]≤min（m，n），且AB为m×m矩阵，则当m＞n时，由r（AB）≤n，知AB为不可逆矩阵，故必有|AB|=0．

相关内容