设f′(lnx)=1+x,则f(x)=( )。A. B. C. D.
题目
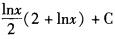
B.
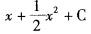
C.
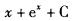
D.
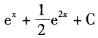
相似考题
更多“设f′(lnx)=1+x,则f(x)=( )。”相关问题
-
第1题:
设f'(lnx)=1+x,则f(x)等于: 答案:C解析:提示:设lnx=t,得f'(t)=1+et形式,写成f'(x)=1+ex,积分。
答案:C解析:提示:设lnx=t,得f'(t)=1+et形式,写成f'(x)=1+ex,积分。 -
第2题:
设'(x)=x+lnx,求f(x).答案:解析:
-
第3题:
设f'(lnx) = 1 + x,则f(x)等于( )。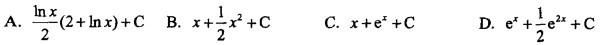 答案:C解析:提示:令t =lnx,再两边积分。
答案:C解析:提示:令t =lnx,再两边积分。 -
第4题:
设函数f(x)=2lnx+ex,则f′(2)等于( )A.E
B.1
C.1+e2
D.In2答案:C解析:【考情点拨】本题考查了函数在一点的导数的知识点.【应试指导】
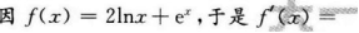
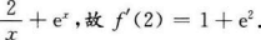
-
第5题:
设f(x)可导,F(x)=f(x)[1-|ln(1+x)|],则f(0)=0是F(x)在x=0处可导的( )《》( )A.充分必要条件
B.充分但非必要条件
C.必要但非充分条件
D.既非充分条件也非必要条件答案:A解析:
-
第6题:
如果f(x)=e-x,则[f′(lnx)/x]dx等于:()
- A、-(1/x)+c
- B、1/x+c
- C、-lnx+c
- D、1nx+c
正确答案:B -
第7题:
单选题设y=f(lnx)ef(x),其中f可微,则dy=( )。A[f′(lnx)ef(x)+f′(x)f(lnx)ef(x)]dx
B[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx
C[f(lnx)ef(x)/x+f(x)f(lnx)ef(x)]dx
D[f′(lnx)ef(x)/x+f(x)f(lnx)ef(x)]dx
正确答案: B解析:
由y′=f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x),得dy=[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx。 -
第8题:
单选题已知f′(ex)=xe-x,且f(1)=0,则f(x)=( )。A(lnx)2/4
B(lnx)/2
C(lnx)/4
D(lnx)2/2
正确答案: B解析:
采用换元积分法,ex=t,则x=lnt,f′(t)=(lnt)/t,即f′(x)=(lnx)/x,故f(x)=∫[(lnx)/x]dx=(lnx)2/2+C,又f(1)=0,得C=0,则f(x)=(lnx)2/2。 -
第9题:
单选题设f(x)=sinx,f[φ(x)]=1-x2,则φ(x)=( )。Aarcsin(1-x)
Barcsin(1+x)
Carcsin(1-x2)
Darcsin(1+x2)
正确答案: C解析:
因sin(arcsinx)=x,又知f(x)=sinx,f[φ(x)]=1-x2,故φ(x)=arcsin(1-x2)。 -
第10题:
单选题设y=f(lnx)ef(x),其中f可微,则dy=( )。A[f(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx
B[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx
C[f′(lnx)ef(x)/x+f(x)f(lnx)ef(x)]dx
D[f(lnx)ef(x)/x+f(x)f(lnx)ef(x)]dx
正确答案: A解析:
由y′=f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x),得dy=[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx。 -
第11题:
单选题设f′(lnx)=1+x,则f(x)等于()A(1nx/2)(2+lnx)+c
Bx+(1/2)x2+c
Cx+ex+c
Dex+(1/2)e2x+c
正确答案: A解析: 暂无解析 -
第12题:
单选题已知f′(ex)=xe-x,且f(1)=0,则f(x)=( )。Alnx
Blnx/2
C(lnx)2
D(lnx)2/2
正确答案: D解析:
采用换元积分法,ex=t,则x=lnt,f′(t)=(lnt)/t,即f′(x)=(lnx)/x,故f(x)=∫[(lnx)/x]dx=(lnx)2/2+C,又f(1)=0,得C=0,则f(x)=(lnx)2/2。 -
第13题:
设f'(lnx) =1+x,则f(x)等于:
A.lnx/2(2+lnx)+c B. x+1/2x2+c
C. x+ex+c D. ex+1/2e2x+c答案:C解析:提示:设lnx=t,得f'(t)=1+et形式,写成f'(x) =1+ex ,积分。 -
第14题:
设随机变量X的概率密度f(x)满足f(1+x)=f(1-x),且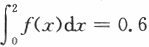 =
=
A.A0.2
B.0.3
C.0.4
D.0.5
答案:A解析:
-
第15题:
设函数f(x)=(1+x)ex,则函数f(x)( )A.有极小值
B.有极大值
C.既有极小值又有极大值
D.无极值答案:A解析:【考情点拨】本题考查了函数极值的知识点.【应试指导】
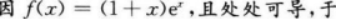

-
第16题:
设lnx是f(x)的一个原函数,则f'(x)=( )
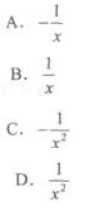 答案:C解析:
答案:C解析: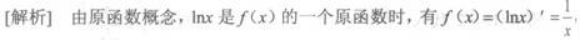
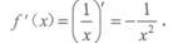
-
第17题:
设4/(1-x2)·f(x)=d/dx[f(x)]2,且f(0)=0,则f(x)等于:()
- A、(1+x)/(1-x)+c
- B、(1-x)/(1+x)+c
- C、1n|(1+x)/(1-x)|+c
- D、1n|(1-x)/(1+x)|+c
正确答案:C -
第18题:
设f′(lnx)=1+x,则f(x)等于()
- A、(1nx/2)(2+lnx)+c
- B、x+(1/2)x2+c
- C、x+ex+c
- D、ex+(1/2)e2x+c
正确答案:C -
第19题:
单选题如果f(x)=e-x,则[f′(lnx)/x]dx等于:()A-(1/x)+c
B1/x+c
C-lnx+c
D1nx+c
正确答案: C解析: 暂无解析 -
第20题:
单选题已知f′(ex)=xe-x,且f(1)=0,则f(x)=( )。A(lnx)/2
B(lnx)2/2
C(lnx)2
Dlnx
正确答案: B解析:
采用换元积分法,ex=t,则x=lnt,f′(t)=(lnt)/t,即f′(x)=(lnx)/x,故f(x)=∫[(lnx)/x]dx=(lnx)2/2+C,又f(1)=0,得C=0,则f(x)=(lnx)2/2。 -
第21题:
填空题设y=f(lnx)ef(x),其中f可微,则dy=____。正确答案: [f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx解析:
由y′=f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x),得dy=[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx。 -
第22题:
单选题设4/(1-x2)·f(x)=d/dx[f(x)]2,且f(0)=0,则f(x)等于:()A(1+x)/(1-x)+c
B(1-x)/(1+x)+c
C1n|(1+x)/(1-x)|+c
D1n|(1-x)/(1+x)|+c
正确答案: A解析: 计算等号右边式子,得到f′(x)表达式。计算不定积分。 -
第23题:
单选题设y=f(lnx)ef(x),其中f可微,则dy=( )。A[f′(lnx)ef(x)/x-f′(x)f(lnx)ef(x)]dx
B-[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx
C[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx
D-[f′(lnx)ef(x)/x-f′(x)f(lnx)ef(x)]dx
正确答案: A解析:
由y′=f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x),得dy=[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx。
